Encapsulation theory: the minimised, uniformly hidden radial branch.
Edmund Kirwan*
www.EdmundKirwan.com
Abstract
This paper investigates how the violational elements of a single, radial branch uniformly distributed in hidden elements should be distributed so as to minimise the branch's potential coupling.
Keywords
Encapsulation theory, radial encapsulation, branch, potential coupling.
1. Introduction
As was shown in [3], the potential coupling of a radial branch is not minimised when all its hidden and violational elements are uniformly distributed over all its disjoint primary sets and instead if the violational elements are uniformly distributed then there exists a function which dictates how to non-uniformly distribute the hidden elements such that the potential coupling falls below that of a uniformly-distributed branch.
Similarly, there exists a function which dictates how to distribute the violation elements of a branch so as to minimise its potential coupling given a uniform distribution of hidden elements.
This paper investigates this second, violational distribution function.
This paper considers sets of radial information-hiding only.
2. Selected branch potential couplings
Consider the branch shown in figure 1, which was also investigated in [3], showing a branch of three disjoint primary sets, where the information-hiding and the information-hiding violation of the sets are shown within their representative symbols.
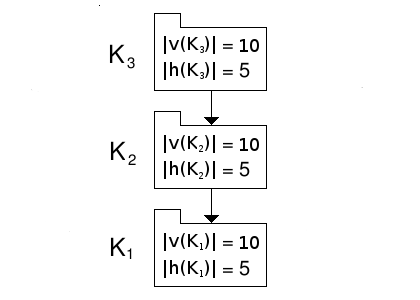
Figure 1: A branch of three disjoint primary sets.
Thus,
taking the root set, K1, for example, we see
that K1 has 10 violational elements,
=10,
and 5 hidden elements,
=5.
As was shown in [3], the branch's potential coupling is: 510+360+210=1080.
We know that, in the absolute encapsulation context, potential coupling is minimised (ignoring A.M.C.s) when both the violational and hidden element are distributed uniformly over all sets. Let us test to see whether this also holds in the radial encapsulation context: let us move a violational element from K1 to K3, see figure 2.
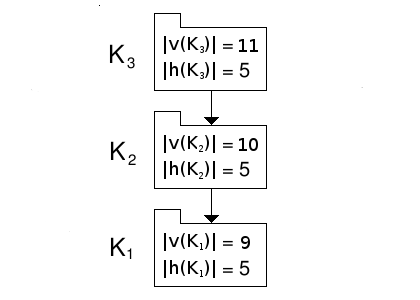
Figure 2: A branch of three disjoint primary sets, one element migrated.
Let us calculate the potential coupling of the branch in figure 2.
The potential coupling of K3 is the sum of its internal and external potential couplings. The internal potential coupling of K3 is the total number of contained elements multiplied by this number minus one, i.e., 16x15=240. The external potential coupling of K3 is the total number of contained elements multiplied by the total number of violational elements it can see "below" it, i.e., 16x(10+9)=304. So the potential coupling of K3 is 240+304=544.
The internal potential coupling of K2 is 15x14=210. K2 can only see 9 violational elements "below" it, so its external potential coupling is 15x9=135. So the potential coupling of K2 is 210+135=345.
The internal potential coupling of K1 is 14x13=182 and K1 has not external potential coupling so its potential coupling is just 182.
The branch's total potential coupling has now fallen from 1080 to 544+345+182=1071.
Thus by moving a violational element, thereby rendering the branch non-uniformly distributed in violational elements, we have reduced the branch's potential coupling. We note that the branch is still uniformly distributed in hidden elements. This then raises the obvious question: given a branch that is uniformly distributed in hidden elements, what distribution of violational elements will minimise its potential coupling?
It can be shown that, to attain the minimum potential coupling in this case, the number of violational elements in the ith disjoint primary set is given by the following equation (see proposition 10.18):
With this equation we can calculate the number of violational elements in each of the three sets examined above to minimise the potential coupling.
K3 should contain the following number of violational elements:
K2 should contain the following number of violational elements:
K1 should contain the following number of violational elements:
The branch thus configured is shown in figure 3.
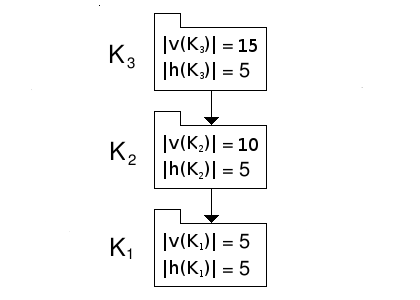
Figure 3: A branch non-uniformly distributed in violational elements with minimised potential coupling.
Calculating the potential coupling of this minimised branch we see the following.
The potential coupling of K3 is 20x19+20x15=680.
The potential coupling of K2 is 15x14+15x5=285.
The potential coupling of K1 is 10x9=90.
The branch's total potential coupling is 680+285+90=1055, down from the original, uniformly distributed figure of 1080.
4. Conclusion
When a branch is uniformly distributed in hidden elements, its minimum potential coupling is not achieved by also uniformly distributing its violational elements. Instead, an equation describes the violational element distribution to achieve this minimum potential coupling and this equation suggests placing more violational elements towards the higher part of the branch than the lower.
5. Appendix A
5.2 Definitions
[D10.1]
Given a branch B of
disjoint
primary sets, the number of elements in B, denoted
,
is the sum of the number of hidden and violational elements in each
disjoint primary set constituting the branch, or:
[D10.2] Given a branch B
ofdisjoint
primary sets, the number of violational elements in B,
denoted
,
is the sum of the number of violational elements in each disjoint
primary set constituting the branch, or:
5.2 Propositions
Proposition 10.1
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of
,
the number of elements in the ith primary
set,
,
is given by:
Proof:
By definitions [D1.2], [D1.6] and [D1.7] of [1], the elements in Ki are those in the intersection of Ki with H and V, or:
(i)
By definition [D1.1] in [1], H and V are disjoint so taking the cardinality of (i) gives:
(ii)
We presume that each disjoint
primary set has an information-hiding of,
that is:
(iii)
Substituting (iii) into (ii) gives:
QED
Proposition 10.2
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the internal potential coupling of the ith
primary set,
,
is given by:
Proof:
By definition [D1.2] in [1],
given a primary set Qi the internal
potential coupling
is
given by:
(i)
By proposition 10.1, the number
of elements in the ith primary set,,
is given by:
(ii)
Substituting (ii) into (i) gives:
=
QED
Proposition 10.3
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the following holds:
Proof:
From
definition [D10.1], the number of elements in B,
denoted,
is the sum of hidden and violational elements in each disjoint
primary set constituting the branch, or:
(i)
By proposition 10.1, the number
of elements in the jth primary set,
,
is given by:
(ii)
Substituting (ii) into (i) gives:
=
=
(iii)
Taking an arbitrary i
such that
,
then it follows that:
(iv)
Substituting (iv) into (iii) gives:
QED
Proposition 10.4
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the external potential coupling of the ith
primary set,
,
is given by:
Proof:
Consider the root primary set Q1.
As Q1 is the root primary set, however, all other disjoint primary sets in this branch are subsets of Q1, thus the external potential coupling of the root disjoint primary set is 0.
The external potential coupling of the Q2 is then the number of ordered pairs that may be formed towards K1.
The external potential coupling of the Q3 is the number of ordered pairs that may be formed towards K1 and K2, etc.
Thus:
=
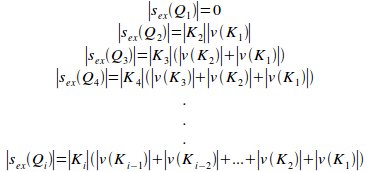
(i)
By proposition 10.3, the following holds:
(ii)
Substituting (ii) into (i) gives:
(iii)
By proposition 10.1, the number
of elements in the ith primary set,,
is given by:
(iv)
Substituting (iv) into (iii) gives;
=
QED
Proposition 10.5
Given
a branch B of
elements
and of
disjoint
primary sets, with each disjoint primary set having an
information-hiding of
,
the external potential coupling of the ith
primary set,
,
is given by:
Proof:
By proposition 10.4, the
external potential coupling of the ith
primary set,,
is given by:
(i)
By definition:
(ii)
Substituting (ii) into (i) gives:
QED
Proposition 10.6
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the potential coupling of the ith primary
set,
,
is given by:
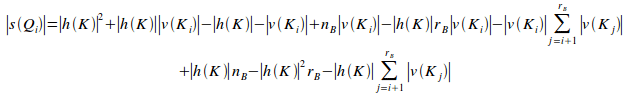
Proof:
By proposition 10.2, the
internal potential coupling of the ith
primary set,
,
is given by:
(i)
By proposition 10.5, the
external potential coupling of the ith
primary set,,
is given by:
(ii)
By proposition 8.7 in [3], the potential coupling of Qi is the sum of the external potential coupling sets of Qi and the internal potential coupling of Qi, or:
(iii)
Substituting (i) and (ii) into (iii) gives:
=
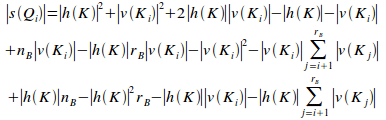
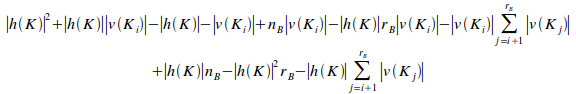
QED
Proposition 10.7
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the number of violational elements in the first disjoint primary
set,
,
is given by:
Proof:
From
definition [D10.1], the number of elements in B,
denoted,
is the sum of hidden and violational elements in each disjoint
primary set constituting the branch, or:
(i)
By proposition 10.1, the number
of elements in the jth primary set,,
is given by:
(ii)
Substituting (ii) into (i) gives:
=
=
(iii)
By definition:
(iv)
Substituting (iv) into (iii) gives:
QED
Proposition 10.8
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the square of the number of violational elements in the first
disjoint primary set,
,
is given by:
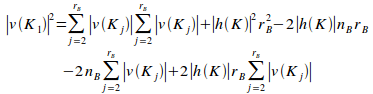
Proof:
By proposition 10.7, the number
of violational elements in the first disjoint primary set,,
is given by:
(i)
Squaring (i) gives:
=
QED
Proposition 10.9
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the potential coupling of the first primary set,
,
is given by:
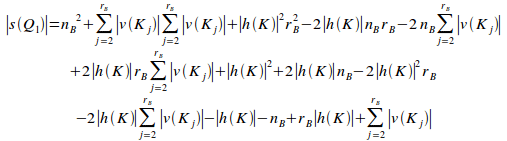
Proof:
By definition [D1.2] in [1],
given primary set Q1 the internal potential
coupling
is
given by:
(i)
By proposition 10.1, the number
of elements in the first primary set,
,
is given by:
(ii)
Substituting (ii) into (i) gives:
=
(iii)
By proposition 10.7, the number
of violational elements in the first disjoint primary set,,
is given by:
(iv)
By proposition 10.8, the square
of the number of violational elements in the first disjoint primary
set,,
is given by:
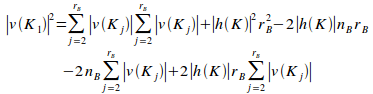(v)
Substituting (iv) and (v) into (iii) gives:
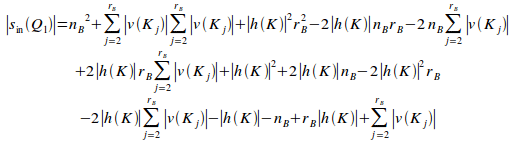(vi)
By definition, the first
disjoint primary set has no external potential coupling,
therefore
and
therefore (vi) is also the equation for the potential coupling of the
first disjoint primary set.
QED
Proposition 10.10
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the potential coupling of B is minimised when:
Proof:
To find the number of violational elements that minimises the potential coupling of branch B we must differentiate the potential coupling of B with respect to the total number of violational elements and set equal to zero, that is:
(i)
By definition [D10.2], the
number of violational elements in B, denoted,
is the sum of the number of violational elements in each disjoint
primary set constituting the branch, or:
(ii)
Substituting (ii) into (i) gives:
(iii)
By definition I SHOULD PROVE THIS ????????????????????????xxx, the potential coupling of branch B is equal to the sum of the potential coupling of all its primary sets, or:
(iv)
Substituting (iv) into (iii) gives:
(v)
=
QED
Proposition 10.11
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the sum of the potential coupling of the first primary set Q1
with respect to the number of violational elements in all disjoint
primary sets of B is given by:
Proof:
By proposition 10.9, the
potential coupling of the first primary set,
,
is given by:
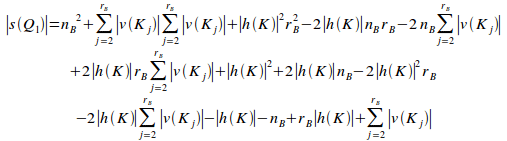(i)
As there are no v(K1)
terms (i) even after expansion then differentiating this with respect
togives:
(ii)
For i > 1,
differentiating this with respect to
gives:
(iii)
By proposition 10.7, the number
of violational elements in the first disjoint primary set,,
is given by:
(iv)
Substituting (iv) into (iii) gives:
(v)
Taking the sum of the potential coupling of Q1 with respect to the number of violational elements in all disjoint primary sets of B gives:
(vi)
Substituting (ii) and (v) into (vi) gives:
=
=
=
QED
Proposition 10.12
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
differentiating the potential coupling of the mth
primary set,
,
where m > 1, with respect the number of violational
elements in any randomly chosen ith disjoint
primary gives:
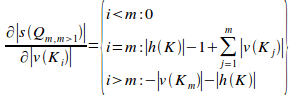
Proof:
By proposition 10.6, the
potential coupling of the mth primary set,,
is given by:
(i)
We now wish to differentiate (i) with m > 1 with respect to the number of violational elements in any randomly chosen ith disjoint primary set, but there is a problem: the solution is not unique, and instead depends on how i relates to m. Thus we must consider three separate solutions.
Firstly, differentiating (i) with respect to the number of violational elements in the ith disjoint primary set such that i < m gives:
(i)
Differentiating (i) with respect to the number of violational elements in the ith disjoint primary set such that i = m gives:
(ii)
By proposition 10.3, the following holds:
(iii)
And from (iii) it follows that:
(iv)
Substituting (iv) into (ii) gives:
(v)
Finally, differentiating (i) with respect to the number of violational elements in the ith disjoint primary set such that i > m gives:
(vi)
QED
Proposition 10.13
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the sum of the potential coupling of all primary sets
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
such that i = m gives:
Proof:
By equation (v) of proposition
10.12, differentiating the potential coupling of the mth
primary set,,
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
such that i = m gives:
(i)
As we are only interested in the case of , then taking the sum over all Ki will just result in those terms where i = m; in other words, there is only one ith term per m in which we are interested, or:
(ii)
Taking the sum from
of
(ii), however, gives:
=
=
=
=
(iii)
But:
And:
(iv)
Substituting (iv) into (iii) gives:
(v)
By equation (iii) of proposition 10.7:
(vi)
Substituting (vi) into (v) gives:
=
QED
Proposition 10.14
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the sum of the potential coupling of all primary sets
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
such that i > m gives:
Proof:
By equation (vi) of proposition
10.12, differentiating the potential coupling of the mth
primary set,,
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
such that i > m gives:
(i)
We are interested in evaluating (i) over all i, m > 1. We note, however, that i > m only for values of m that are less than rB, so the upper value of m is rB - 1. That is, we need to calculate:
Let us first take the sum of (i) over all i > m, giving:
(ii)
As the neither of the terms on the right-hand side of (i) is a function of i and there are (rB - m) terms in which i > m, then:
=
(iii)
Taking the sum from
of
(iii) gives:
=
=
(iv)
By equation (iii) of proposition 10.7:
(v)
Substituting (v) into (iv) gives:
=
=
QED
Proposition 10.15
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the sum of the potential coupling of all primary sets
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
where i > 1 gives:
Proof:
By definition:
(i)
By proposition 10.12:
(ii)
By proposition 10.13, the sum of
the potential coupling of all primary sets
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
such that i = m gives:
(iii)
By proposition 10.14, the sum of
the potential coupling of all primary sets
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
such that i > m gives:
(iv)
Substituting (ii), (iii) and (iv) into (i) gives:
=
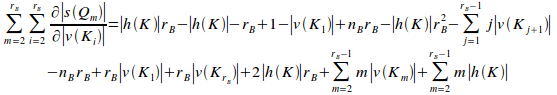
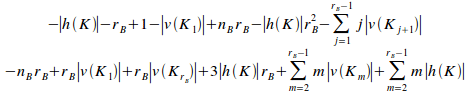(v)
By definition:
=
(vi)
Substituting (vi) into (v) gives:
=
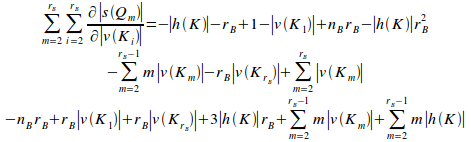
(vii)
By equation (iii) of proposition 10.7:
(viii)
Substituting (viii) into (vii) gives:
=
QED
Proposition 10.16
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the number of violational elements in the first disjoint primary set
that minimises the branch's potential coupling is given by:
Proof:
By proposition 10.10, the potential coupling of B is minimised when:
(i)
By proposition 10.15, the sum of
the potential coupling of all primary sets
where m > 1, with respect to the number of violational
elements in the ith disjoint primary set
where i > 1 gives:
(ii)
By proposition 10.11, the sum of the potential coupling of the first primary set Q1 with respect to the number of violational elements in all disjoint primary sets of B is given by:
(iii)
Substituting (ii) and (iii) into (i) gives:
=
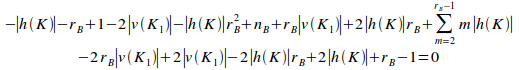
(iv)
By definition:
=
(v)
Substituting (v) into (iv) gives:
=
=
=
=
=
QED
Proposition 10.17
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the number of violational elements in the ith
disjoint primary set that minimises the branch's potential coupling
is given by:
Proof:
By definition I SHOULD PROVE THIS ????????????????????????xxx, the potential coupling of branch B is equal to the sum of the potential coupling of all its primary sets, or:
(i)
Choosing an arbitrary i
such that
we
can re-write (i) as:
(ii)
Taking the derivative of both
sides of (ii) with respect togives:
(iii)
Setting (iii) equal to 0 will yield the minimum potential coupling of branch B with respect to the number of violational elements in the Ki.
By proposition 10.12,
differentiating the potential coupling of the mth
primary set,,
where m > 1, with respect the number of violational
elements in any randomly chosen ith disjoint
primary gives:
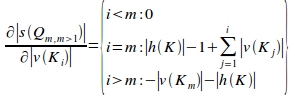(iv)
By equation (v) in proposition 10.11,
(v)
Substituting (iv) and (v) into (iii) gives:
=
=
=
=
QED
Proposition 10.18
Given
a branch B ofelements
and ofdisjoint
primary sets, with each disjoint primary set having an
information-hiding of,
the number of violational elements in the ith
disjoint primary set that minimises the branch's potential coupling
is given by:
Proof:
By proposition 10.16, the number of violational elements in the first disjoint primary set that minimises the branch's potential coupling is given by:
(i)
By proposition 10.17, the number of violational elements in the ith disjoint primary set that minimises the branch's potential coupling is given by:
(ii)
Substituting (i) into into (ii) gives:
=
=
=
QED
6. References
[1] - "Encapsulation theory fundamentals," Ed Kirwan, www.EdmundKirwan.com/pub/paper1.pdf
[2] - "Encapsulation theory: the minimised, uniformly hidden radial branch," Ed Kirwan, www.EdmundKirwan.com/pub/paper10.pdf
[3] “Encapsulation theory: the minimised, uniformly violational radial branch," Ed Kirwan, www.EdmundKirwan.com/pub/paper9.pdf
*© Edmund Kirwan 2010. Revision 1.0, March 28th 2010. (Revision 1.0: March 28th 2010.) All entities may republish, but not for profit, all or part of this material provided reference is made to the author and title of this paper. The latest revision of this paper is available at [2].