Abstract

This paper proposes a theory of encapsulation, taking the internationally standardized definition of that term and establishing the encapsulated set: a set of sets of elements the relationship between which is objectively determinable. This relationship is the potential coupling, the maximum potential number of source code dependencies that can exist between program units in a software system. The potential coupling of various, simple systems is examined in an attempt to demonstrate how potential coupling changes as program units are encapsulated among different configurations of subsystems.

Keywords

Encapsulation theory, information hiding, encapsulation, potential coupling.

1. Introduction

This paper arguably presents little that is new and rather examines the current practice of encapsulation from a shifted perspective. Two definitions - those of encapsulation itself and of information-hiding - are used as a foundation on which to build a logical framework that may be used in turn to analyse real-world structures and to identify, and correct, possible structural flaws.

2. Foundation

The Reference Model of Open Distributed Processing [10] - the International Organisation for Standardization's International Standard - defines the following five concepts:

Entity: Any concrete or abstract thing of interest.

Object: A model of an entity. An object is characterised by its behaviour and, dually, by its state.

Behaviour (of an object): A collection of actions with a set of constraints on when they may occur.

Interface: An abstraction of the behaviour of an object that consists of a subset of the interactions of that object together with a set of constraints on when they may occur.

Encapsulation: the property that the information contained in the model of an entity is accessible only through interactions at the interfaces supported by the model.

Given that an entity model has a behaviour and that the interfaces it supports grant access only to a subset this behaviour, and given that encapsulation enforces interaction via only these interfaces, we can logically conclude that encapsulation grants access to some of an entity model's behaviour but not to all.

This paper proposes that the behaviour subset to which access is forbidden by encapsulation is information hidden, a term coined by Parnas [2], who argues that modules should be designed to hide both difficult decisions and decisions that are likely to change. (We must make a terminological leap to bridge the twenty-six-year gap between the Parnas and ISO papers: what Parnas describes as a module this section shall describe as an entity model. The connection between a decision and a behaviour is less precise, but we can say both that a collection of actions may certainly entail the making of decisions and that any decision may be subsumed within a behaviour: thus this section will interpret Parnas's decisions as elements of behaviours).

Given that a programmer may re-implement any entity model's behaviour at any time, all behaviour has some likelihood of change and it is precisely this change potential that the programmer considers when choosing which behaviour subsets should be accessible to clients and which should not, that is, when choosing how to encapsulate the behaviour.

Four aspects of information hiding are noted.

Firstly, it is a human that designs modules and it is a human that evaluates whether a decision is difficult or likely to change. Whatever information hiding concerns, therefore, it is practised for the benefit of humans, not machines; in software engineering, this is equivalent to saying that information hiding concerns source code (or models if model-driven development is practised), not compiled/run-time code. A high-level computer language may support information hiding, but once that program is compiled, the resulting executable code need not reflect the information hiding strategies of the original source.

Secondly, the designing-to-hide strategy is essentially one of restriction rather than liberation. The hiding of a decision necessarily entails a reduction of system information from the point of view of some observer.

Thirdly, the target of any proposed restriction is not the decisions being hidden themselves but the relations between modules involving those decisions. Parnas is not advocating the elimination of decisions but the elimination of inter-module relations towards those decisions. As he further clarifies, "The relation we are concerned with is uses or depends upon."

Fourthly, information hiding concerns the potential as well as the immediate. As already mentioned, all decisions have some likelihood of change; those decisions with the highest change potential are best candidates for information hiding.

Thus we claim: information hiding restricts potential source code dependencies, i.e., it restricts source code dependencies that have not yet been implemented. Given that information hiding is a key part of encapsulation, then we can also claim that encapsulation entails, to some degree, the restriction of potential source code dependencies.

Consider the system of four program units in figure 1.

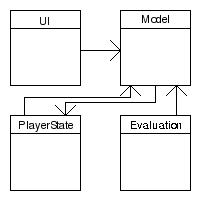
Figure 1: System of four program units.

Here, both the UI and the Evaluation program units have a dependency towards the Model program unit. The PlayerState and Model program units share two dependencies.

Figure 1 thus shows a system of four dependencies. We do not know the encapsulation strategy governing this system but we know that any encapsulation strategy will concern potential - and not just actual - source code dependencies.

We may thus ask: how many potential dependencies are possible within this system? What is the maximum potential number of dependencies that these four program units could generate? The answer is shown in figure 2.

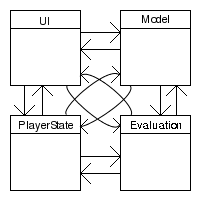
Figure 2: Maximum interconnectedness.

A count reveals that the four program units could generate twelve potential dependencies. These twelve dependencies do not, of course, exist in the system, but they could; we say that, independent of the number of actual dependencies the system has, it has twelve potential dependencies. (Throughout this document, we consider only non-transitive dependencies.)

As mentioned, there is no single definition of complexity in computer science, yet intuitively we might feel that the system (were the dependencies actual) in figure 2 is more complex than that of figure 1, because, all else being equal, figure 2 shows more dependencies.

Let us, therefore, axiomatically define the potential coupling of a system as the maximum potential number of dependencies between program units of that system in its current configuration.

We thus say that the system shown in figure 1 has a potential coupling of 12.

3. Encapsulation and information hiding

Before examining potential coupling further, we must attempt to define some measurements of encapsulation. These definitions will be introduced, furthermore, in a stepwise manner: beginning quite informally so as to guide the student through familiar terminology, and concluding with a formal definition used for rigorous proofs.

As has already been proposed, information hiding is only a part of encapsulation. Another aspect of encapsulation is that of containment, as can clearly be seen in its ISO definition (once again): the property that the information contained in an entity model is accessible only through interactions at the interfaces supported by the model.

Containment immediately suggests that which is container and that which is contained: initially, analyses shall be performed considering the contained to be program unit and the containers to be subsystems. We shall therefore define our first measure of encapsulation as simply the number of program units contained in a subsystem.

Let us also define, "Information hiding," as the restricting of forming dependencies on any particular program unit within a subsystem from outside that subsystem. This gives us our second measure of encapsulation, namely, the number of program units within a subsystem that are not visible outside that subsystem.

Note that, according to the above, two program units within the same subsystem cannot be information hidden from one another.

4. A preliminary appraisal

Returning to figure 2, we have seen that the four, unencapsulated program units generate twelve dependencies. This is an example of an unencapsulated system, in that the four program units are not separated into subsystems. In fact, given any unencapsulated system, G, of n program units, the potential couplingis given by:

(See proposition 1, though this equation has long been known in set theory.) In our example, n = 4, and we see that:

4² - 4 = 16 - 4 = 12

It is clear, then, that the potential coupling of an unencapsulated system is proportional to the square of the number of its program units, or that the potential coupling rises quadratically with the number of program units involved. This is also the upper ceiling of potential coupling for any given n program units: it is impossible for any system to generate a higher potential coupling than this.

Here we gain our first insight into the nature of potential coupling: for unencapsulated systems, potential coupling scales quadratically as program units are added. Figure 3 shows the potential coupling for unencapsulated systems of one up to one hundred program units, it is thus said to show the potential coupling response of these systems.

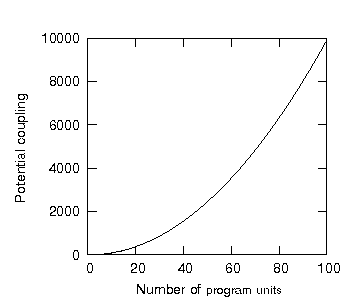
Figure 3: Potential coupling as a function of the number of program units in an unencapsulated system.

The potential coupling for unencapsulated systems, as we can see from figure 3, scales more than linearly. In general, however, any complexity response rising faster than linearly threatens to make large systems disproportionately more difficult to create than small systems. We may then wonder what an ideal potential coupling response for a system might be.

Such an ideal response would show a reduction of potential coupling with the addition of program units, yet this is clearly impossible, as potential coupling measures the maximal potential connectedness of the program units of a system, and each new program unit must by definition involve the addition of at least one dependency within the system or else the newly added program unit cannot meaningfully be said to be part of that system.

A more realistic, desired response, therefore, would entail adding as little potential coupling as possible with the addition of program units. The rest of this paper is concerned with the search for such a desired response. We shall do so by performing some simple experiments within three encapsulation contexts.

5. Encapsulation contexts and experiment

An encapsulation context is a set of constraints on the formation of potential ordered pairs (that is, dependencies) within a set.

The first encapsulation context examined is the absolute encapsulation context; this context ignores, from the point of view of dependency formation, the recursive declaration of subsystems within subsystems, treating all subsystems as though they were declared in isolation from one another.

This paper focuses on this context; the other two encapsulation contexts we shall review - in far less detail - are the one-dimensional hierarchical encapsulation context and the two-dimensional hierarchical encapsulation context, both defined later in the paper.

To explore the potential coupling of systems residing within the absolute encapsulation context, we shall perform the three experiments.

The first experiment is called, "The fixed-system experiment." This experiment takes a fixed number of program units and a fixed number of subsystems, and examines how the potential coupling of the system changes as program units are distributed over the subsystems.

The second experiment is called, "The varied-set experiment," which takes a fixed number of program units and examines how the potential coupling of the system changes as program units are uniformly distributed over an increasing number of subsystems, that is, as the system moves from one uniform distribution to another.

The third experiment is called, "The system-growth experiment," which takes a number of systems composed of increasing numbers of program units and examines how the minimum potential coupling of the configuration increases as more program units are added.

(We have, indeed, already performed one such system-growth experiment: figure 3 showed the results of the this experiment for an unencapsulated system, the graph showing the quadratic nature of the potential coupling response of the first 100 unencapsulated systems.)

6. Absolute encapsulation

Absolute encapsulation means that the information hiding of a subsystem is independent of its relationship with all other subsystems (a point to which we shall return in section 6.7). A system may be hierarchically structured yet not be hierarchically encapsulated (in fact Java systems, in advance of the introduction of super-packages, are usually hierarchically structured but not hierarchically encapsulated).

Take the system described in figure 4, which shows four subsystems: a, b, c and d, with c declared within b.

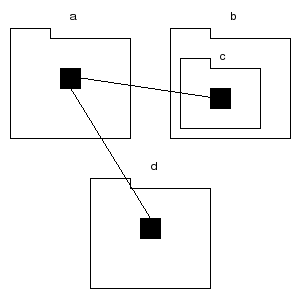
Figure 4: Recursive/nested structure.

Figure 4 shows a hierarchically structured system, as c is contained within b, but in an absolutely encapsulated system, such structure has no effect the ability of program units to form dependencies. In the diagram, the program unit in a can form dependencies on the program unit in c just as it can on the program unit in d.

6.1. The fixed-system experiment

This experiment will attempt to answer the question: is the potential coupling of a system minimised when it is uniformly distributed, that is, when its program units are uniformly distributed over its over subsystems?

Consider four program units and two subsystems. We shall examine all possible configurations in which these four program units can be distributed over the two subsystems.

We must first, however, chose an encapsulation strategy that will remain constant throughout the experiment. Our encapsulation strategy will simply state the maximum number of program units that are visible outside a subsystem (as we shall see later, this is achieved in Java by declaring a class public). We shall chose to have only one program unit per subsystem visible outside that subsystem; that is, all but one program unit will be information-hidden within each subsystem. (As we shall discuss later, this conserving of number of public programs per subsystem is an isoledensal transformation.) The program units that are information-hidden will be coloured white; the other program units (the, "Public," program units) will be coloured black.

Let us begin by encapsulating all four program units in one subsystem while leaving the other subsystem empty. See figure 5 for the resulting potential coupling and note that, for pictorial convenience, the arrows indicating dependency directionality have been omitted.

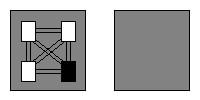
Figure 5: Four program units in 1 subsystem.

Here we see twelve potential dependencies between the four program units; the potential coupling is twelve, just as it was when the program units were unencapsulated (see figure 2).

Next, we shall examine the configuration whereby three program units reside in one subsystem and one in the other, see figure 6.

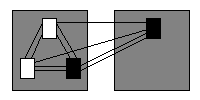
Figure 6: Three program units in one subsystem.

Here, we see ten potential dependencies; the potential coupling is ten, two fewer than in figure 5. Why are there fewer dependencies than in figure 5?

The reason there are fewer potential dependencies concerns the two white program units on the left. As before, they are information hidden within their subsystem, but in figure 5, this information hiding is irrelevant, as all program units within a subsystem are visible to one another and thus can form dependencies towards one another; only program units outside the subsystem are restricted from forming dependencies towards information hidden program units.

In figure 6, however, the program unit on the right now cannot form dependencies towards those information-hidden program units in the subsystem on the left.

It is because information hiding has come into play in figure 6, restricting one program unit's ability to form dependencies towards two others, that the potential coupling has fallen by two.

Let us proceed and examine the system with the four program units uniformly distributed over two subsystems, see figure 7.

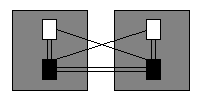
Figure 7: Two program units in each subsystem.

Now, there are only eight potential dependencies; the configuration in figure 7 has a potential coupling of eight, two fewer than in figure 6, and a full four dependencies fewer than the original figure 5.

Again, the reason for this decline in potential coupling concerns information hiding. Some scrutiny of the evolving configurations reveals that the collapse of a program unit's ability to form bi-directional dependencies with others within its own subsystem has been unmatched by the rise in its ability to form unidirectional dependencies towards the visible program units of the other subsystem.

In figure 5, each program unit can form bidirectional dependencies towards three others; in figure 6, each program unit can form bidirectional dependencies towards only two others; in figure 7, each program unit could can form bidirectional dependencies towards only one other program unit.

This asymmetry between forming bidirectional dependencies within a subsystem and unidirectional dependencies without is at the heart of encapsulation theory and we shall now further refine potential coupling to reflect it.

We shall define the internal potential coupling as the number of potential dependencies formed by program units on one another within a subsystem, and we shall define the external potential coupling as the number of potential dependencies formed by program units towards program units outside their subsystem. The potential coupling of a subsystem is then the sum of these two terms.

Our earlier scrutiny can now be re-phrased as follows: the fall in the system's overall potential coupling stems from the collapse of the internal potential coupling's being unmatched by the rise in external potential coupling.

Before looking deeper into this relationship, we should conclude the experiment, though it turns out that there is little more to learn as continuing to move program units into the subsystem on the right immediately confronts us with mirror-images of earlier configurations; figure 8, for example, shows one program unit in the subsystem on the left and three in the subsystem on the right.

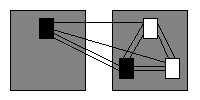
Figure 8: Three program units in one subsystem.

Figure 8 has the same potential coupling as that of figure 6 (reflecting the images has no effect on the number of dependencies formable). Figure 7, therefore, exhibits the lowest potential coupling of all the configurations. Recall that the question to be answered by this experiment was: is the potential coupling of a system minimised when it is uniformly distributed? The answer appears to be yes (and indeed is yes when public program units are uniformly distributed).

The potential coupling equations governing the system reflect this answer.

The equation for the internal potential coupling of a subsystem (see proposition 1.2.) takes the same form as that already encountered for an unencapsulated system, namely, where K is subsystem of n program units, then the internal potential coupling,, is (loosely):

The external potential coupling of a subsystem is less elegant, but given here for completeness (see proposition 1.4.):

Although not immediately apparent, there is a difference between the two equations in terms of order. The equation for external potential coupling contains no powers, that is, it is linear. This can be seen more clearly by noting that the three terms on the right-hand-side of the equation are all constants, thus by arbitrarily assigning constant values to these terms, we can re-write the equation as:

All the powers on the right-hand-side can thus be seen to be 1; there are no a² or c³ terms, for example.

This is why uniform distribution tends to minimise potential coupling: because the quadratic nature of internal potential coupling will tend to dominate the linear nature of external potential coupling whenever program units cluster unevenly into subsystems.

So, we have tentatively concluded that a system's potential coupling - when the number of public programs per subsystem is conserved - is minimised by its being uniformly distributed (again, this is certainly the case when the public program units are uniformly distributed). When examining four program units, it is clear that having two program units in two subsystems is the only uniform distribution available; but what if there are many possible uniform distributions?

What if we want to encapsulate, for example, twelve program units to minimise potential coupling: which uniform distribution is best? Six program units in two subsystems? Four program units in three subsystems?

Indeed, is there any configuration that minimises potential coupling?

6.2. The varied-set experiment

Let us perform our second experiment, the aim of which is to investigate whether there exists a configuration that minimises potential coupling, that is, whether the potential coupling of a specific system tends to be minimised by that system's being in a specific uniform distribution.

Consider a system of twelve program units. We shall divide this system up into an increasing number of subsystems such that an equal number of program units will be in each subsystem at any given time. We shall, again, enforce the encapsulation strategy of having only one program unit per subsystem visible outside that subsystem.

First, we shall examine a system that is unencapsulated, see figure 9. Again for pictorial convenience, the remaining figures of this paper will represent both a unidirectional and a bidirectional dependency with just one line.

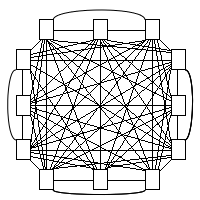
Figure 9: Twelve program units unencapsulated.

The unencapsulated system in figure 9 has a potential coupling of 132. This is as predicted by our previously established equation for the potential coupling of an unencapsulated system:

We shall now view the system encapsulated into two subsystems of six program units each, thus there will be just two program units (coloured black) in the system that are visible to all else, whereas five program units in each subsystem will be visible only to one another. See figure 10.

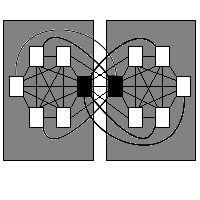
Figure 10: Two subsystems, six program units in each.

With the twelve program units encapsulated in two subsystems, the potential coupling falls to just 72.

Let us make an incautious hypothesis at this point: we shall predict that the potential coupling falls as the number of subsystems increases. Figure 11 shows the twelve program units encapsulated in three subsystems of four program units each.

Figure 11: Three subsystems, four program units in each.

The potential coupling of figure 11 is 60, in line with our hypothesis so far: the potential coupling has fallen as we increase the number of subsystems. Next we shall look at the twelve program units uniformly encapsulated in four subsystems, see figure 12.

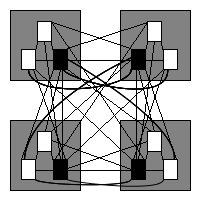
Figure 12: Four subsystems, three program units in each.

Here, our hypothesis falters slightly, as the potential coupling of figure 6 is 60, the same as the potential coupling of the twelve program units encapsulated into three subsystems. We shall continue the experiment regardless. Figure 13 shows the twelve program units encapsulated in six subsystems.

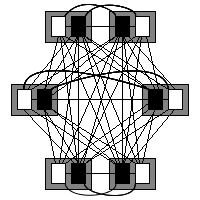
Figure 13: Six subsystems, two program units in each.

With six subsystems, the potential coupling rises to 72 and our naive hypothesis disintegrates. It seems that increasing the number of subsystems does not automatically decrease the minimum potential coupling of a system. Figure 14, finally, shows each program unit alone in its own subsystem.

Figure 14: Twelve subsystems, one program unit in each.

In figure 14, the potential coupling has risen to the original value of 132. The results of this experiment are shown most clearly by drawing a graph of the potential coupling against the number of subsystems into which the twelve program units were uniformly encapsulated, see figure 15.

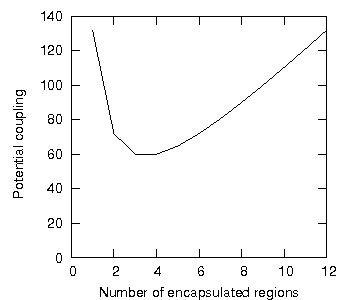
Figure 15: Potential coupling versus number of subsystems.

With figure 15, then, we seem to have answered our question: does there exist a system configuration that minimises potential coupling? From the graph, it appears that both three and four subsystems minimise the potential coupling of this system, at least for our given isoledensal constraint of having one program visible per subsystem.

In fact, for any system in an absolute encapsulated context with n program units equally distributed over all subsystems and with the same number of externally visible program units, d, in each subsystem, it turns out that the number of subsystems, r_ild, at which the potential coupling is isoledensally minimised is given by:

(See proposition 1.12.) Thus, for 12 program units (n=12) each with one program unit externally visible (d=1), r_ild== 3.46, though, obviously, we can only have whole numbers of subsystems in any real system.

6.3. The system-growth experiment

Our third and final experiment for the absolute encapsulation context is to examine how the potential coupling of the potential-coupling-minimised configuration increases as more program units are added.

We shall examine all systems composed of one to one hundred program units. For each system, we shall find the minimum isoledensal potential coupling (see proposition 1.14) and plot this minimum as a function of the number of program units.

Figure 16 shows the resulting graph; on this graph we shall also plot the same one hundred systems whose program units are unencapsulated (that is, the quadratic response already shown in figure 3). In figure 16, the potential coupling of the unencapsulated systems is the higher line, whereas the potential coupling of the absolute encapsulation context is the lower line.

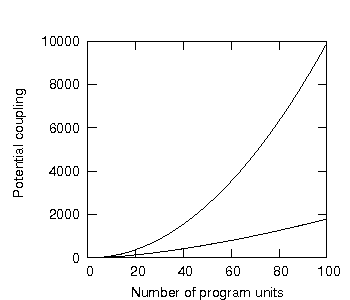
Figure 16: Unencapsulated and absolute encapsulation context potential coupling as a function of the number of program units.

Figure 16 shows the degree to which encapsulation can reduce the potential coupling of a system: for a system of just one hundred program units, an unencapsulated system expresses over five times more potential coupling than an encapsulated system.

Examining of the equation of proposition 1.14 reveals that minimised isoledensal potential coupling is proportional to or that the order of the equation is O(n^1.5). Recall that the potential coupling equation for an unencapsulated system was quadratic, or of order O(n²). This reduction of order 0.5 is responsible for the differences between the two graphs in figure 16.

6.4. The information-hiding violation

It is perhaps worth examining the role of d in the above equations in more detail. This variable represents the the number of program units within a subsystem that are visible outside that subsystem. In Java, for example, a class declared with the access modifier public is visible outside the package in which it resides:

package com.rail;

public class Train {

...

}

Here the Train class is visible outside the com.rail package. (Actually, Java also supports the protected access modifier which also makes classes public outside their resident package, but we shall ignore this identifier in this analysis.) We shall define such visibility to be a information-hiding violation, and the variable d above is merely the number of information-hiding violations of a subsystem. The number of information-hiding violations per subsystem is called the specific information-hiding violation of a system. If Train is the only class defined as public within the com.rail package, then the number of information-hiding violations of the com.rail package is 1 (d=1). If there are two classes defined as public in com.rail, then the number of information-hiding violations of the com.rail package is 2 (d=2), etc..

Figure 15 presented the results of the varied-set experiment, showing the potential coupling of 12 program units as the system moved from one uniform distribution to another. A general equation for this graph can be derived (see proposition 1.8) which calculates the potential coupling as a function of the number of program units, subsystems and number of information-hiding violations. Figure 17 plots this equation by showing, for example, the potential coupling as 100 program units are distributed over a number of subsystems (note the similarity with figure 15), again with one information-hiding violation per subsystem (d=1).

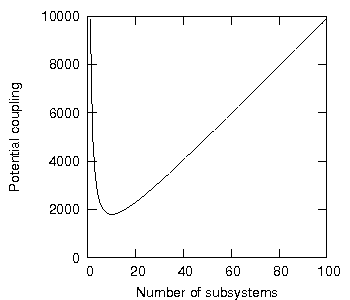
Figure 17: Potential coupling of 100 program units versus number of subsystems.

It may also be seen from the graph that the number of subsystems at which the potential coupling is minimised is, again, given by:

We shall now examine what happens when there are two information-hiding violations per subsystem (d=2), and then three (d=3) and then four (d=4); see figure 18.

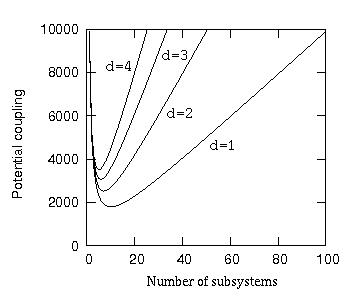
Figure 18: Potential coupling of 100 program units versus number of subsystems with increasing number of public program units per subsystem.

Two details are noteworthy.

Firstly, as the number of information-hiding violations per subsystem rises, the minimum isoledensal potential coupling also rises. This means that the more public program units reside in the system, the higher the minimum isoledensal potential coupling will be.

Secondly, as the number of information-hiding violations per subsystem rises, the number of possible subsystems over which the program units can be distributed falls.

This becomes obvious when we consider that, with a requirement of one information-hiding violation per subsystem, then the minimum number of program units per subsystem is one, and thus the system can be distributed over a maximum of 100 subsystems. With a requirement of two information-hiding violations per subsystem (d=2), then the minimum number of program units per subsystem is two, and thus the system can be distributed over a maximum of 50 subsystems.

6.5. Real software systems

6.5.1. Minimum potential coupling for d=1

Let us define equivalence by saying that two systems are equivalent if they have the same number of program units and subsystems and they have the same specific information-hiding violation.

The systems studied to this point have generally been uniformly distributed because a uniformly distributed system with d=1 has a lower potential coupling than any equivalent, non-uniformly distributed system (see proposition 1.11). Real systems, however, tend not to have only one program unit public per subsystem, and their subsystems usually do not all contain the same number of program units.

Yet even real systems must obey the laws of encapsulation in that they are not free to express any potential coupling without check; real systems may not express a potential coupling outside the range established by propositions 1.1 and 1.14 (with d=1).

To visualise this, let us take 1000 randomly generated systems. The creation of these systems will be subject to three constraints: (i) each system must have exactly 100 program units; (ii) each system must contain a random number of subsystems, between 1 and 100; and (iii) each subsystem must contain a random number of public and private program units (though each must have at least one public program unit).

So, for example, a system of three subsystems - each having 12, 7 and 53 private program units respectively and each having 5, 2 and 21 public program units respectively - would be a valid system; a system of 57 subsystems would be a valid system, and so on.

Let us also take the plot of the minimum isoledensal potential coupling of a system of 100 program units uniformly distributed, as shown in figure 17, and superimpose on it our 1000 random system configurations, see figure 19, where each cross represents the potential coupling response of one random system.

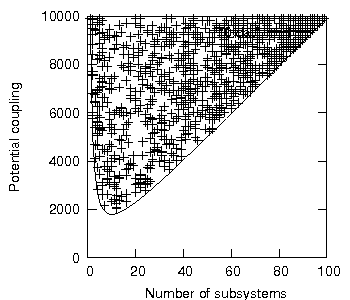
Figure 19: The potential coupling of 1000 random systems.

As can be seen from figure 19, none of the 1000 systems breaches the gradient mandated by proposition 1.8. Here, we may interpret the potential coupling gradient not as a line but as an edge sweeping out an area - the potential coupling surface - onto which every system must map to a single point (and over which each system will trace a trajectory as it develops).

Thus is illuminated for the programmer some real constraints to which programs are (and, indeed, always have been) subjected.

As we shall see, it is proposition 1.11 that provides the connection between real and theoretical systems, allowing us to use the mathematical tools of uniformly-distributed systems to gain insight into the non-uniformly-distributed systems of real software.

6.5.2. Minimum potential coupling for d>1

Most of the randomly generated systems in figure 19, however, have d>1. It would be satisfying if it were proven that the minimum isoledensal potential coupling of a uniformly-distributed system of d=2, for example, was also the lowest possible potential coupling of the equivalent, non-uniformly distributed systems. This, however, is not the case.

For d>1, there exist non-uniformly distributed systems - called anomalous minimised configurations (A.M.C.s) - whose potential coupling is less than that of their equivalent uniformly-distributed systems. Take, for example, the A.M.C. in table 1.

	# Private program units	# Public program units
Subsystem 1	33	12
Subsystem 2	5	50

Table 1: The first A.M.C.

Table 1 shows a system of 100 program units (n=100), two subsystems (r=2) and a specific information-hiding violation of 31 (d=31). The potential coupling of this system (see propositions 1.2 and 1.4) is 7860. The minimum isoledensal potential coupling of the equivalent, uniformly-distributed system (see proposition 1.14) is 7935.

A detailed investigation of A.M.C.s would take us too far from the fundamentals being examined here and so is covered in [11].

6.5.3. Instability

Void.

6.5.4. Isoledensal configuration efficiency

Another aspect of encapsulation theory's view of real-world systems concerns program functionality. Just as an all-purpose definition of complexity eludes us, unfortunately so too does an all-purpose definition of functionality: functionality is loosely considered a measure of how much a program does; the more a program does, the more functionality it has. It is also - again loosely - the case that the more program units a system has the more functionality it delivers. We can certainly say that the addition of program units may increase a system's functionality.

The potential coupling equations basically express potential coupling as a function of (among other things) the number of program units in a system, thus it can be viewed as an equation of conversion of potential coupling to functionality and vice versa. The history of software engineering has largely been that of creating increasingly large programs and then managing the ensuing, increasingly large complexity. The potential coupling equation, however, offers us a means of turning this history on its head and asking: given a certain potential coupling, how much functionality can we efficiently extract?¹

It is this efficiency that is of interest. Recall that the typical minimum isoledensal potential coupling graph shown in figure 17 shows a system with 100 program units differing only in how those program units are encapsulated into subsystems: if functionality is a function of the number of program units, then there will be no change in the functionality of a system as the same 100 program units are re-distributed over subsystems; and yet proposition 1.12 shows that there is a minimum isoledensal potential coupling for a system of a given specific information-hiding violation (A.M.C.s notwithstanding), regardless of whether the system's expressed potential coupling approaches this minimum.

Combining these two ideas leads to the proposal that any potential coupling above the minimum is a rise² in a form of system complexity without a necessary rise in concomitant functionality.

This leads to the concept of isoledensal configuration inefficiency, which we shall define as that proportion of potential coupling a system expresses over and above its minimum isoledensal potential coupling given a specific information-hiding violation; the point being that all inefficient potential coupling is reducible, in theory, to zero. There are two ways of doing this: either by reducing the system's overall potential coupling through re-encapsulation; or by maintaining the system's overall potential coupling but adding program units (and thus lowering the inefficient potential coupling by increasing functionality, a process that may continue until the inefficient potential coupling is zero, after which the addition of program units must cause the overall potential coupling to rise again).

The equation for configuration inefficiency c_i is thus:

Where:

= actual system potential coupling

= minimum system isoledensal potential coupling

= maximum system potential coupling

Though it is more usual to express this as an efficiency c_e which is simply:

Thus the configuration efficiency ranges from 0 to 1. A configuration efficiency of 1 means that the system is expressing its minimum isoledensal potential coupling (all of its potential coupling is converted to functionality); a configuration efficiency of 0 means that the system is expressing the maximum possible potential coupling (its potential coupling is converted to functionality with minimum efficiency).

Encapsulation theory suggests a raft of other software metrics - not least the potential coupling itself - yet just one is mentioned here: the percentage information-hiding violation (I.H.V.), the number of public program units divided by the total number of program units, multiplied by 100. Given that this is, in some sense, a crude measurement of a system's information hiding, this metric offers an excellent, "First appraisal," of a system; a high percentage I.H.V. usually obviates the need to check the configuration efficiency.

Let us examine some open-source, Java software systems from sourceforge [6]. The projects will be taken more or less at random though Jboss and Eclipse are included specifically for their size.

We shall parse them at the third-set (i.e., class/package level, see section 6.6) with a free, downloadable tool, Fractality: Free Edition [5], which computes a range of encapsulation theory metrics; see table 2 (where, "I.C.E.," stands for, "Isoledensal configuration efficiency.") Note that (i) the systems were parsed in their entirety, no attempt was made to separate dedicated source code from included, third-party libraries; (ii) the systems are presumed to reside within absolute encapsulation contexts; (iii) the source code is presumed to be human-manipulated (not, for example, generated from human-manipulated models, see introduction).

	Num. elements	Potential coupling	I.C.E.	I.H.V.
SEdit	135	16956	0.09	93%
Fractality3	240	19042	0.86	25%
HSQLdb	283	61633	0.37	72%
Jasper Reports	316	99540	0	100%
JBPM	366	133590	0	100%
Manta- Ray	384	132298	0.12	89%
Blue Marine	468	194991	0.13	89%
Jboss	4244	17619836	0.02	98%
Eclipse	39114	933916300	0.4	61%

Table 2: Sample systems and associated metrics.

The systems depicted in table 2 present too small a sample for us to draw definitive conclusions (a broader, empirical survey is being researched). We note some casual observations, however:

• Both JasperReports and JPBM have made all their classes public, thus attaining minimum configuration efficiency.

• MantaRay has more classes than JBPM and yet expresses a lower potential coupling; MantaRay achieved this through its higher configuration efficiency.

• Despite its astronomically high potential coupling, Eclipse has one of the highest configuration efficiencies of the selection.

• Few systems have a high configuration efficiency.

Also, though not apparent from the statistics shown, Jboss re-encapsulated to its theoretical minimum isoledensal potential coupling given its current number of classes and specific information-hiding violation, would reduce its current potential coupling from 17 million to 1 million.

As a final note on the utility of configuration efficiency, consider that to minimise potential coupling the number of program units in a subsystem should be proportional to the total number of program units (proposition 1.15). It is impractical, however, to redistribute program units during software development each time the number of program units change, so the common programming practice is to enforce a maximum number of program units per subsystem. This proves to be a good strategy for managing potential coupling; there is a cost, but the configuration efficiency remains approximately scale invariant for a wide range of systems, a desirable quality in any encapsulation strategy. Figure 24, for example, shows a graph of a system of increasing number of program units and its corresponding configuration efficiency (which levels off at 0.91), the constraint being that system is allowed to have at most ten program units per subsystem (again, d=1).

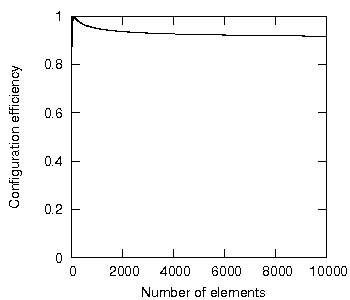
Figure 24: Configuration efficiency with ten program units per subsystem.

6.6. Interpretations

So far we have discussed the encapsulation of program units within subsystems. We shall now generalise these concepts by taking advantage of the terminology of set theory.

We shall consider each program unit within a subsystem to be an element of a set. Those sets are themselves subsets of the overall set that represents the entire system. We shall introduce the term, "disjoint primary set," loosely defined as a subset containing elements each of which is distinguishable by membership of that disjoint primary set. Essentially, the subsystems discussed so far are disjoint primary sets and the program units inside these subsystems are the elements within the disjoint primary sets. An encapsulated set, then, is any set whose every element resides within an disjoint primary set.

The mathematics of encapsulation theory are independent of computer programming and dependent only on the underlying set theory; that such a theory is relevant to computer programming is due to our ability to view program units residing within subsystems as elements residing within a set.

It therefore does not seem unreasonable to take this view at least one stage deeper for just as a subsystem is a set of elements so too is a program unit a set of functions.

Thus we have another set and all that has been said so far about program units within subsystems also applies to functions within program units, where functions may be considered elements and program units may be considered subsets.

In this case, information hiding is the restricting of forming dependencies on any particular function within a program unit. To take a Java example again, where a program unit is a class and a function is method, the following class has two information-hiding violations (methods go() and stop()) because both methods can be called by classes outside the Car class:

class Car {

public void go() {…};

void stop() {…};

private void alarm() {…};

}

Encapsulation theory can therefore answer questions such as: given 100 functions and a requirement for just two functions to be visible outside each program unit, what number of program units will isoledensally minimise the potential coupling of this system? The answer, by proposition 1.12 again, is:

It may also be reasonable to take this view yet another stage deeper still as there is a long-standing tradition of viewing even lines of code as a set. In his landmark paper on cyclomatic complexity [9], Thomas McCabe describes source code where, "Each element in the graph corresponds to a block of code in the program where the flow is sequential and the arcs correspond to branches taken in the program."

We may adopt McCabe's view (and thus risk similar critique [1]), establishing a third set whereby blocks of sequential program flow are considered elements and functions are considered subsets. This view is particularly attractive in that most programming languages allow only a single point-of-entry into a function, and thus we may consider the first block of sequential flow to be the only information-hiding violation of any function (d=1).

We thus arrive at the set stack, see figure 25.

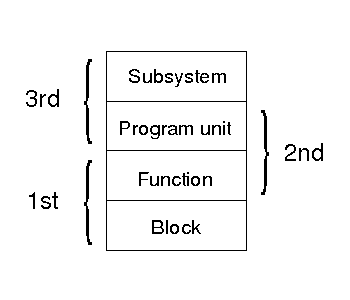
Figure 25: Set stack.

In figure 25, we see the set stack of the absolute encapsulation context. The first⁴ is the block/function set, where blocks are encapsulated into functions; the second is the function/program unit set, where functions are encapsulated into program units; the third is the program unit/subsystem set, where program units are encapsulated into subsystems.

Given that, usually, d=1 for the first set, there is higher probability that software at the first set will have a higher configuration efficiency than software at the higher sets.

At the second set, we note that there is a tendency to make functions public solely that they may be unit tested, in the belief that this has no consequence at the third set given that the parent program units remain private within their subsystems. Encapsulation theory shows, however, that although increasing d at the second set decreases the number of subsystems needed at the third set, the sum of the potential couplings of the two sets increases with increased d at the second set.

6.7. New information hiding

So far we have considered only the absolute encapsulation context, which has a proven lower limit to its potential coupling (proposition 1.14). Encapsulation contexts are defined by the type of information hiding they employ; we shall now investigate whether it is possible to attain even lower potential coupling in a different encapsulation context. We shall first rename the information hiding discussed so far, "Absolute information hiding."

The new information hiding needed to further reduce potential coupling is, "Relative information hiding."

According to both types of information hiding, a program unit defined as information hidden within its subsystem is forbidden to receive dependencies from outside that subsystem. This is inviolable. It is with respect to, "Public," program units that the two types differ.

According to absolute information hiding, a program unit defined as visible outside its subsystem is allowed to receive dependencies from all program units in all other subsystems. This, for example, is the standard treatment in Java, where a class declared as public is visible to all classes in all other packages.

According to relative information hiding, however, a program unit defined as visible outside its subsystem is allowed to receive dependencies only from those program units in other subsystems that enjoy a special relationship with the target subsystem.

What this, "Special relationship," means is usually defined by a system's software architecture, often imposed by consensual and extra-linguistic design rule. Java does not (at least, again, in advance of the introduction of super-packages) support relative information hiding but a Java system may, simply by specifying appropriate guidelines to programmers.

A common design rule used to establish relative information hiding, for instance, is the imposition of software layers, a layer usually being a collection of subsystems. This layer is then defined in relation to other software layers precisely so that relationships between layers can be controlled, a typical rule being of the form, "Lower layers may not depend on the program units of higher layers," where, "Lower," and, "Higher," refer either to technical abstraction, appropriate orientation. See figure 26.

Figure 26: Software layers.

In figure 26, we see three layers, each holding four subsystems; the arrows indicate that the dependencies between layers are allowed only from higher to lower layers. Though usually called, "Layering," we shall call this a, "One-dimensional hierarchical encapsulation context."

We shall briefly analyse this and the two-dimensional encapsulation hierarchical context to which relative information hiding gives rise, though note that, as opposed to absolute information hiding - which essentially takes only one form - there are endless variations of relative information hiding, and the mathematics of even the simplest variations are not well understood.

7. One-dimensional hierarchical encapsulation

In our brief overview of the one-dimensional hierarchical encapsulation context, we make two assumptions.

Firstly, we shall assume that layers do not contain other layers.

Secondly, we shall assume that layers do not admit differential information hiding of their encapsulated subsystems: all subsystems of a layer are visible to client layers without any being able to declare themselves as visible only to other subsystems within the layer itself.

7.1. The fixed-system experiment

Again, we shall perform the fixed-system experiment to investigate whether the potential coupling of a specific system is minimised by its being uniformly distributed.

Consider twelve subsystems distributed over three layers. We shall begin with ten subsystems in layer 1 (the bottom layer) and one subsystem in each of the other two layers. Then we shall put nine subsystems in layer 1, two subsystems in layer 2 and one subsystem in layer 1, etc..

We shall perform this experiment using a computer simulation rather than drawing out the dependencies by hand. The results are shown in figure 27.

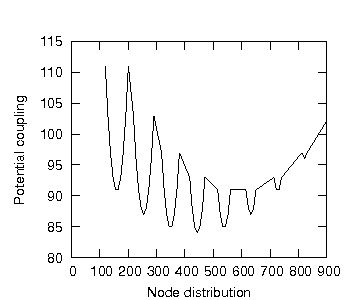
Figure 27: Distributing 12 subsystems over 3 layers.

Figure 27 is slightly difficult to interpret but the data confirm that the system's potential coupling is minimised when there are four subsystems in each layer (hence the minimum at 4-4-4), that is, when the subsystem are uniformly distributed overall the layers.

Although it has not been proven that uniform distribution minimises all one-dimensional hierarchical encapsulated systems, we shall take this experiment as evidence to support the conjecture.

7.2. The varied-set experiment

We shall perform our second experiment, the varied-set experiment, to attempt to establish whether there exists a system configuration (in this case, a particular number of layers) that minimises the potential coupling of a system.

Consider again a system of 100 program units. We shall divide this system up into an increasing number of layers, such that the elements will be uniformly distributed over any number of subsystems and these subsystems will be uniformly distributed over the layers.

First, we shall examine a system of one layer. Within this one layer, we shall examine all configurations of the 100 elements distributed over 1 to 100 subsystems, and we shall record the configuration with the lowest potential coupling.

Second, we shall examine a system of two layers. Within these two layers, we shall examine all configurations of the 100 elements distributed over 1 to 100 subsystems, and we shall record the configuration with the lowest potential coupling.

Next, we shall examine a system of three layers, etc., all the way to a system with 100 layers, with one subsystem per layer and one program unit per subsystem.

Each subsystem will have an information-hiding violation of 1 (d=1). Program units of subsystems in each layer will be able to form dependences towards subsystems in the same layer, and all layers below. Program units in layer 3, for example, will be able to form dependencies towards program units in other subsystems in layer 3, and on those in layers 2 and 1.

The result of this minimum potential coupling plotted against increasing numbers of layers is shown in figure 28.

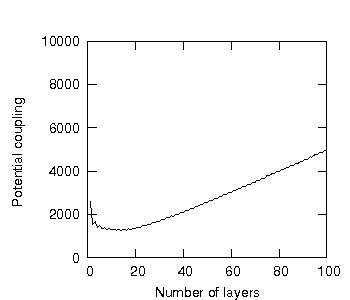
Figure 28: Distributing 100 program units over 1-100 layers.

Figure 28 suggests that there is indeed a number of layers which - when program units and subsystems are uniform distributed - minimises the potential coupling of the system.

The number of layers is, of course, a parameter with which we were not confronted when we examined the absolute encapsulation context. Given here for completeness and without proof is the equation for the potential coupling of such a one-dimensional hierarchical encapsulation:

Where:

n = number of program units

r = number of subsystems

L = number of layers

r_L = number of subsystems per layer

L_d = dependency layer penetration

d = information-hiding violation per subsystem

7.3. The system-growth experiment

In this experiment, again, we shall examine all systems composed of one to one hundred program units. For each system, we shall find the configuration with the minimum potential coupling such that all program units are uniformly distributed over subsystems and all subsystems are uniformly distributed over layers.

As in the previous experiment, each subsystem will have an information-hiding violation of 1 (d=1) and program units of subsystems in each layer will be able to form dependences towards subsystems in the same layer, and all layers below.

We shall then plot this minimum potential coupling as a function of increasing numbers of program units. This is shown in figure 29, plotted against the same results already shown for the unencapsulated and one-dimensional hierarchical encapsulated contexts so far encountered (in figure 16).

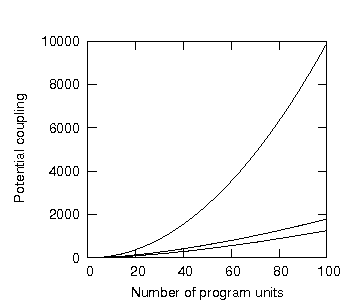
Figure 29: Unencapsulated, absolute encapsulated and layered potential coupling responses.

Figure 29 shows the minimum potential coupling of systems containing 1 to 100 program units. The upper line is the unencapsulated system; the next line down is the absolute encapsulation context; the lowest line shows the one-dimensional hierarchical encapsulation context. As is evident, the layering of one-dimensional hierarchical encapsulation appears to reduce the minimum potential coupling even beyond an absolute encapsulation context.

8. Two-dimensional hierarchical encapsulation

The one-dimensional hierarchical encapsulation context is one-dimensional in that only a single degree of restriction exists in forbidding dependencies between layers; essentially, a layer is either, "Above," or, "Below," another layer.

A simple two-dimensional hierarchical encapsulation context is achieved by taking the system described in figure 26 once again and adding the design rule that, for example, "Subsystems may not form dependencies on subsystems to their right." This effectively carves the figure into a two-dimensional plane, whereby the dependencies allowable are determined by a subsystems position in the x-axis (up or down the graphic) and the y-axis (position across the graphic).

Here, however, we hit a limitation of the layer as a second-class citizen of the software construct: simply put, whereas the imposition of dependency-restriction upon a collection of subsystems seems reasonable, programmers tend to baulk at the arbitrariness of assigning meaning to sub-collections of subsystems within layers.

We shall, therefore, investigate the more robust concept of a two-dimensional hierarchy based on recursively-defined subsystems. To do so, we must first present some simple graphical conventions. Consider the three subsystems shown in figure 30.

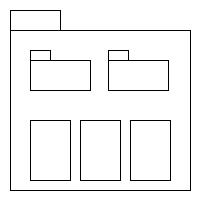
Figure 30: A subsystem containing two other subsystems.

Figure 30 shows a large subsystem graphic enclosing two smaller subsystem graphics and three program unit graphics. This represents the larger subsystem's containing two subsystems and three program units. The larger subsystem is said to be the parent of the two smaller subsystems; the two smaller subsystems are said to be the children of the larger subsystem. If we concentrate solely on the subsystem graphics and ignore the program units, this containment is often drawn as a tree showing the two child subsystems above the parent subsystem, as in figure 31.

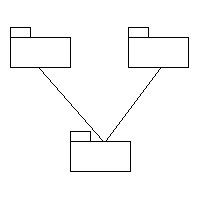
Figure 31: A subsystem containing two other subsystems.

Figure 31 shows the parent subsystem on the bottom (in the root position, to extend the tree metaphor), and its two children on top. As well as the parent-child relationship, we can also define the peer-peer relationship: two subsystems are peers when the share the same immediate parent. Thus the two child subsystems in figure 31 are peer subsystems.

Finally, the span-of-control is defined as the number of children that a parental subsystem has.

Given these simple terms, we may then assess the efficacy with which a two-dimensional hierarchy manages potential coupling once we define the governing dependency constraints. As previously, there is no limit to the number of constrains that we might employ; we could, for example, stipulate that, "No dependencies may be formed between peers," or that, "No dependencies may be formed towards parents;" both design rules would yield interesting results; but we shall not consider these here.

We shall consider the design rule, "Dependencies may not form towards children."⁵ Thus, child subsystems are allowed to form dependencies towards peer subsystems, towards their parents, towards peers of their parents, towards parents" parents, towards peers of parents" parents, etc.. This rule forbids a program unit to form a dependency towards subsystems encapsulated within its own subsystem.

For example, consider the system depicted in figure 32.

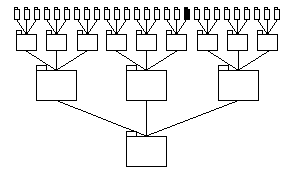
Figure 32: A 2-d hierarchical encapsulation context with a span-of-control of 3.

Figure 32 shows a system of 40 subsystems arranged in a two-dimensional hierarchical encapsulation context. The span-of-control is three: that is, each subsystem contains three other subsystems.

Consider the shaded subsystem of figure 32, lying amid the uppermost (i.e., deepest recursively defined) subsystems: how many subsystems of the rest of the system can it see? The answer is shown in figure 33, whereby each visible subsystem is coloured black.

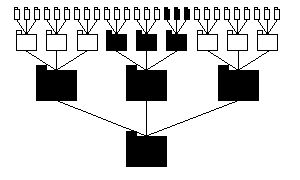
Figure 33: A 2-d hierarchical system showing visibility from a leaf subsystem.

Figure 33 shows that the subsystem highlighted in figure 32 can see three subsystems on each level up from the root subsystem; in total, it can see only 10 of the system's 40 subsystems.

Computer simulation shows that, in fact, a span-of-control of two offers the most effective relative information hiding. Given here for completeness and without proof is the equation for the potential coupling of a two-dimensional hierarchical encapsulation context:

Where:

n = number of program units

r = number of subsystems

k = number of levels

b = span-of-control

d = information-hiding violation per subsystem

8.1. The fixed-system experiment

This experiment, to attempt to establish whether the potential coupling of a two-dimensional hierarchical encapsulation context is minimised by the uniform distribution of program units and subsystems per subsystem, is not performed here and is the subject of on-going research.

8.2. The varied-set experiment

As before, let us perform our second experiment, the varied-set experiment, to try attempt to establish whether there exists a system configuration that minimises the potential coupling of a two-dimensional hierarchical encapsulation context.

Let us take 100 program units and encapsulate them in increasing numbers of subsystems, each with an information-hiding violation of one (d=1), starting with all program units in one subsystem.

We shall then distribute the 100 program units over two subsystems, whereby one subsystem will be the parent of the other and the parent will not be allowed to form any dependencies towards program units within the child subsystem.

Next, we shall distribute the program units over three subsystems, one being the parent of the other two. The fourth subsystem will then be the child of one of the children, and so on, all the while forbidding dependency formation towards child subsystems.

Thus we shall form a two-dimensional hierarchy of subsystems with a span-of-control of two and we shall record the potential coupling of each configuration. The results are shown in figure 34.

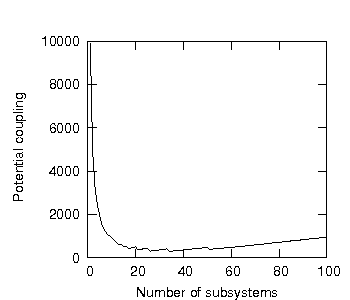
Figure 34: Distributing 100 program units over subsystems in a 2-D hierarchy.

Figure 34 suggests that the potential coupling does indeed fall and then rise again, though not as clearly as with previous experiments (in fact, as the number of subsystems grows in a two-dimensional hierarchy, the potential coupling is quantised into ranges as new levels are created to accommodate the growing number of subsystems: hence the jittery nature of the graph).

Regardless of this somewhat unusual-looking result, the experiment at least suggests that, for any given system of n program units, the system's potential coupling is minimised for some uniform distribution when those subsystems form a two-dimensional hierarchical encapsulation context. (Again, this is not proven.)

Thus we can proceed with our third experiment, to attempt to examine how such systems of increasing numbers of program units express this potential coupling minimum.

8.3. The system-growth experiment

In this experiment we shall examine all systems composed of one to one hundred program units. For each system, we shall find the configuration with the minimum potential coupling such that all program units are uniformly distributed over subsystems and all subsystems are uniformly distributed over a two-dimensional hierarchical encapsulation context with a span-of-control of two.

As in the previous experiment, each subsystem will have a specific information-hiding violation of one (d=1) and the dependency-formation towards child subsystems will be forbidden.

We shall then plot this minimum potential coupling as a function of increasing numbers of program units. This is shown in figure 35, plotted against the same results already collected for this experiment in other contexts.

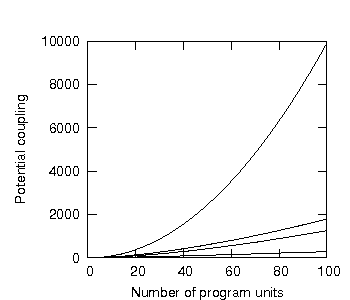
Figure 35: Unencapsulated, absolute, 1-D and 2-D hierarchical encapsulation context potential coupling responses.

Figure 35 shows the minimum potential coupling of systems containing 1 to 100 program units. The upper line is the unencapsulated system; the next line down is the absolute encapsulation context; the third line shows the one-dimensional hierarchical encapsulation context; the lowest line shows the potential coupling expressed by our two-dimensional hierarchical encapsulation context.

The two-dimensional hierarchical encapsulation context suggests a significant improvement over other contenders.

9. CONCLUSIONS

Encapsulation has long been proposed as a useful tool with which to reduce program complexity. This paper has proposed the concept of potential coupling as means to mathematically to explore this claim.

The equations of encapsulation are formulated based on four quantities of a system:

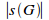• - the potential coupling function.

• n - number of program units

• r - number of subsystems

• d - specific information-hiding violation (i.e., number of public program units per subsystem).

The primary equations examined here were:

1. The maximum potential coupling of an unencapsulated system is given by the equation (proposition 1.11):

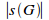   = n(n - 1)

2. The minimum isoledensal potential coupling of a uniformly-distributed system, given a specific information-hiding violation, is expressed when the number of its subsystems is given by (proposition 1.12):

   

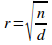
3. The maximum potential coupling of a uniformly-distributed system is expressed when the number of its subsystems is given by (proposition 1.13):

   

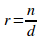
The adage is appropriate once more, "Optimise your encapsulation."

Finally, the mathematics presented here are not restricted to digital physics but apply to any system that can be readily interpreted as a set. A manager wishing to organise 20 people into teams with one team-leader in each team, such that each team may only communicate with the team-leader of the other teams, will find that communication effort will be minimised by the application of proposition 1.12 (giving four teams of five members each).

10. Related work

Coupling and cohesion are introduced in [4]. External potential coupling could be viewed as the coupling defined in [4]; it is more problematic to view internal potential coupling as a form of potential cohesion.

This paper proposes a set theoretic optimal size for software system components ("the Goldilocks conjecture") and proposes equation forms similar to those proposed in [8], which seeks to find an optimised size in terms of defect densities. That paper, however, was then critiqued in [7] , casting doubt on the assumptions made to yield those equations (the same critique cannot be levelled at potential coupling).

11. APPENDIX A

11.1. DEFINITIONS

The propositions described proposed here are based on set theory, so a certain number of standard definitions are assumed. (Note that definitions and propositions presented here govern the absolute encapsulation context only.)

[D1.1] Let G be a set of n elements. Let V be a subset of G called the information-hiding violational set or simply the violational set. Let H be a subset of G, disjoint from V, called the information-hidden set or simply the hidden set. V and H are called secondary sets as a convenient, distinguishing label.

[D1.2] Let all n elements of G be members of V or H. Thus:

[D1.3] Let G also contain r subsets, the i^th subset being Q_i. These r sets are called the primary sets (or primary subsets depending on context) as a convenient, distinguishing label. Each primary set is either disjoint from every other primary set or stands in a subset relation with another primary set. Thus:

[D1.4] Each element of G must be be a member both of a primary and a secondary set. Thus:

[D1.5] Let K_i be the set of all elements in Q_i but not in any primary subset of Q_i. This is called the disjoint primary set of Q_i. Thus:

The set G formed according to definitions [D1.1] to [D1.5] is called an encapsulated set as a convenient, distinguishing label.

[D1.6] Let v(K_i) be the set of all elements of K_i that are also elements of V. This is called the information-hiding violational set of K_i; the information-hiding violation of K_i is the cardinality of this set; an element of this set is called an information-hiding violational element or simply a violational element. Thus:

[D1.7] Let h(K_i) be the set of all elements of K_i that are also elements of H. This is called the information-hiding set of K_i; the information-hiding of K_i is the cardinality of this set; an element of this set is called an information-hidden element or simply a hidden element. Thus:

[D1.8] Let s_in(Q_i) be the set of ordered pairs formed by the Cartesian product of all elements in the disjoint primary set of Q_i with themselves, excluding those pairs resulting from the product of an element with itself. This is called the internal potential coupling set of Q_i; the internal potential coupling of Q_i is cardinality of this set. Thus:

[D1.9] Let s_ex(Q_i) be the set of ordered pairs formed by the Cartesian product of all elements in the disjoint primary set of Q_i with all elements of V that are not also members of the disjoint primary set of Q_i. This is called the external potential coupling set of Q_i; the external potential coupling of Q_i is cardinality of this set. Thus:

[D1.10] Let s(Q_i) be the set of ordered pairs formed by the union of s_in(Q_i) and s_ex(Q_i). This is called the potential coupling set of Q_i; the potential coupling of Q_i is cardinality of this set. Thus:

[D1.11] Let s_in(G) be the set formed by the union of the internal potential coupling of all primary sets of G. This is called the internal potential coupling set of G; the internal potential coupling of G is cardinality of this set. Thus:

[D1.12] Let s_ex(G) be the set formed by the union of the external potential coupling of all primary sets of G. This is called the external potential coupling set of G; the external potential coupling of G is cardinality of this set. Thus:

[D1.13] Let s(G) be the set of ordered pairs formed by the union of s_in(G) and s_ex(G). This is called the potential coupling set of G; the potential coupling of G is cardinality of this set. Thus:

[D1.14] A set is uniformly distributed when each of its disjoint primary subsets contains the same number of elements and has an equal information-hiding violation. Thus for set G of n elements and r disjoint primary sets, G's being uniformly distributed implies:

(i)

(ii)

(iii)

[D1.15] Two sets are equivalent if they have the same number of elements, the same number of subsets and the same information-hiding violation.

Given the above definitions, we may visualise an encapsulated set as figure 36.

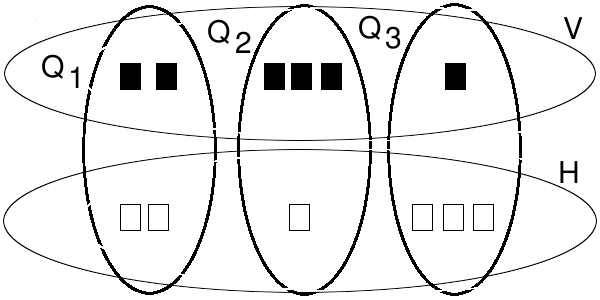
Figure 36: An encapsulated set.

Figure 36 shows the two secondary sets, V and H, and three primary sets, Q₁, Q₂ and Q₃. All of these sets form the set G (not shown). Q₂ has 3 violational elements (the black blocks), that is, the intersection of Q₂ and V is 3. Q₂ has 1 information-hidden element (the white block), that is, the intersection of Q₂ and H is 1.

Figure 37 shows an example of a disjoint primary set.

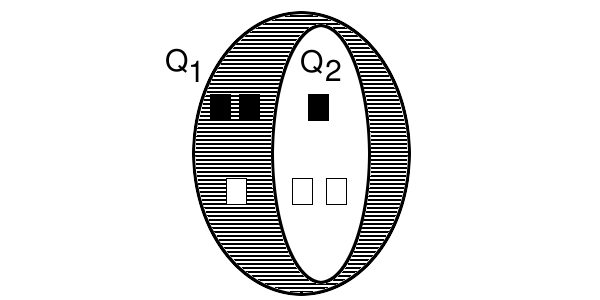
Figure 37: Disjoint primary set.

In figure 37, we see two primary sets, Q₁ and Q₂ (the secondary sets, V and H, are not shown but understood). The disjoint primary set, K₁, of Q₁ is shown in the shaded region: this is all the elements of Q₁ that are not also elements of any subset of Q₁.

Thus Q₁ has 3 violational elements (the black blocks) and 3 information-hidden elements (the white blocks). The disjoint primary set, K₁, however, has just 2 violational elements and 1 information-hidden element. Q₂ has 1 violational element and 2 information-hidden elements.

11.2. Propositions

Proposition 1.1.

Given an encapsulated set G with just one disjoint primary subset, the potential coupling s(G) is given by:

Proof:

To count the maximum possible number of ordered pairs between the n elements is to perform the selection of an order of arrangements of 2 elements, without repetition, selected from the n distinct elements. That is, by definition, the permutation of n elements taken 2 at a time:

QED

Proposition 1.2.

Given a primary set Q_i the internal potential couplingis given by:

Proof:

By definition [D1.8], the internal potential coupling set is given by:

(i)

Permutingelements into ordered pairs givesordered pairs in which the first element of the ordered pair is the same element as the second element of the ordered pair, thus:

(ii)

Taking the cardinality of all elements in (i) gives:

= (iii)

Substituting (ii) into (iii) gives:

=

QED

Proposition 1.3.1

Given an encapsulated set G every element is a member of a disjoint primary set, or:

Proof:

By definition [D1.4], each element of G must be be a member of a primary set. Thus:

(i)

Let Q_i contain arbitrarily many primary subsets, W_j. By definition, any element in Q_i is either in Q_i and not in a primary subset of Q_i or in a primary subset of Q_i. Thus:

(ii)

Substituting (ii) into (i) gives:

(iii)

By definition [D1.5], K_i is the set of all elements in Q_i but not in any subset of Q_i:

(iv)

Substituting (iv) into (iii) gives:

(v)

By definition [D1.3], each primary set is either disjoint from every other primary set or stands in a subset relation with another primary set. Thus:

(vi)

As W_j is also a primary set it also has an associated disjoint primary set, K_j. As this holds for all subsets of Q_i then:

(vii)

Substituting (vii) into (v) gives:

QED

Proposition 1.3.2

Given an encapsulated set G of r primary sets, each disjoint primary set is disjoint from every other, or:

Proof:

By definition [D1.3], each primary set is either disjoint from every other primary set or stands in a subset relation with another primary set:

(i)

By definition [D1.5], K_i is the set of all elements in Q_i but not in any primary subset of Q_i:

(ii)

As K_i contains only elements of Q_i, and K_j contains only members of Q_j, then

(iii)

If Q_i is a primary subset of Q_j, then by (ii) no element in K_i can also be an element in K_j, thus:

(iv)

Similarly:

(v)

Substituting (iii), (iv) and (v) into (i) gives:

QED

Proposition 1.3.3

Given an encapsulated set G of r primary sets, the information-hiding violational set of each disjoint primary set is disjoint from every other, or:

Proof:

By proposition 1.3.2, each disjoint primary set is disjoint from every other, or:

(i)

By definition [D1.6], v(K_i) is the set of all elements of K_i that are also elements of V. Thus v(K_i) is a subset of K_i, or:

(ii)

If any two sets are disjoint, then subsets of both sets are also disjoint, thus:

(iii)

Substituting (ii) into (iii) gives:

Or:

QED

Proposition 1.3.4

Given an encapsulated set G of r primary sets the i^th disjoint primary set being K_i, G is the union of all the disjoint primary sets, or:

Proof:

By proposition 1.3.1, every element of G is a member of some disjoint primary set, or:

(i)

Therefore G must be the union of all disjoint primary sets, or:

QED

Proposition 1.3.5

Given an encapsulated set G of r primary sets and given that the i^th disjoint primary set K_i containselements, the sum of the cardinality of all the disjoint primary sets is total number of elements in G, or:

Proof:

By proposition 1.3.4, G is the union of all disjoint primary sets, or:

(i)

Taking the cardinality of both sides of (i) gives:

= (ii)

By proposition 1.3.2, each disjoint primary set is disjoint from every other, thus:

(iii)

Substituting (iii) into (ii) gives:

QED

Proposition 1.3.6

Given an encapsulated set G of r primary sets, of information-hiding violation V and given that the i^th disjoint primary set K_i containselements and has an information-hiding violational set of v(K_i), the sum of the information-hiding violation of all the primary sets is the cardinality of the information hiding violational set, or:

Proof:

By definition [D1.6], the information-hiding violational set of K_i is given by:

(i)

Taking the union of both sides over all disjoint primary sets gives:

(ii)

By proposition 1.3.4, G is the union of all disjoint primary sets, or:

(iii)

Substituting (iii) into (ii) gives:

(iv)

By definition [D1.1], V is a subset of G, thus:

(v)

Substituting (v) into (iv) gives:

(vi)

Taking the cardinality of both sides of (vi) gives:

(vii)

By proposition 1.3.3, the information-hiding violational set of each disjoint primary set is disjoint from every other, or:

(viii)

It follows from (viii) that the sum of all elements in the intersections of the information-hiding violational sets is 0, or:

(ix)

Substituting (ix) into (vii) gives:

QED

Proposition 1.3.7

Given an encapsulated set G of r primary sets, the information-hiding set of each disjoint primary set is disjoint from every other, or:

Proof:

By proposition 1.3.2, each disjoint primary set is disjoint from every other, or:

(i)

By definition [D1.7], h(K_i) is the set of all elements of K_i that are also elements of H. Thus h(K_i) is a subset of K_i, or:

(ii)

If any two sets are disjoint, then subsets of both sets are also disjoint, thus:

(iii)

Substituting (ii) into (iii) gives:

Or:

QED

Proposition 1.3.8

Given an encapsulated set G of r primary sets, of information-hiding H and given that the i^th disjoint primary set K_i containselements and has an information-hiding set of h(K_i), the sum of the information-hiding of all the primary sets is the cardinality of the information-hiding set, or:

Proof:

By definition [D1.7], the information-hiding set of K_i is given by:

(i)

Taking the union of both sides over all disjoint primary sets gives:

(ii)

By proposition 1.3.4, G is the union of all disjoint primary sets, or:

(iii)

Substituting (iii) into (ii) gives:

(iv)

By definition [D1.1], H is a subset of G, thus:

(v)

Substituting (v) into (iv) gives:

(vi)

Taking the cardinality of both sides of (vi) gives:

(vii)

By proposition 1.3.7, the information-hiding set of each disjoint primary set is disjoint from every other, or:

(viii)

It follows from (viii) that the sum of all elements in the intersections of the information-hiding sets is 0, or:

(ix)

Substituting (ix) into (vii) gives:

QED

Proposition 1.3.9

Given an encapsulated set G and given that the i^th primary set is Q_i, the internal potential coupling set of Q_i is disjoint from the internal potential coupling set of all other primary sets, or:

Proof:

By definition [D1.8], the internal potential coupling set of Q_i is given by:

= (i)

Consider any other primary set, Q_j, such that:

(ii)

Presume thatis not disjoint from. Thus:

(iii)

If (iii) holds, then, given (i) and (ii), there is at least one ordered pair common to bothand, or:

(iv)

But by Proposition 1.3.2. each disjoint primary set is disjoint from every other, or:

(v)

From (v) it follows that there does not exist any element that is a member of both K_i and K_j, or:

Thus (iv) does not follow and so (iii) is false, or:

(vi)

As Q_j in (iii) was considered as any other primary set, we can quantify over all other primary sets, thus:

QED

Proposition 1.3.10

Given an encapsulated set G and given that the i^th primary set is Q_i, the external potential coupling set of Q_i is disjoint the external potential coupling set of all other primary sets, or:

Proof:

By definition [D1.9], the external potential coupling of Q_i is:

= (i)

Consider any other primary set, Q_j, such that:

(ii)

Presume thatis not disjoint from. Thus:

(iii)

If (iii) holds, then, given (i) and (ii), there is at least one ordered pair common to bothand, or:

(iv)

But by Proposition 1.3.2. each disjoint primary set is disjoint from every other, or:

(v)

From (v) it follows that there does not exist any element that is a member of both K_i and K_j, or:

Thus (iv) does not follow and so (iii) is false, or:

(vi)

As Q_j in (iii) was considered as any other primary set, we can quantify over all other primary sets, thus:

QED

Proposition 1.3.11

Given an encapsulated set G and given that the i^th primary set Q_i, the internal potential coupling of G,, is given by:

Proof:

By definition [D1.11], the internal potential coupling set of G is:

(i)

Taking the cardinality of both sides of (i) gives:

= (ii)

By proposition 1.3.9, the internal potential coupling set of any primary set is disjoint from every other internal potential coupling set, thus:

(iii)

Substituting (iii) into (ii) gives:

QED

Proposition 1.3.12

Given an encapsulated set G and given that the i^th primary set Q_i, the external potential coupling of G,, is given by:

Proof:

By definition [D1.12], the external potential coupling of G is:

(i)

Taking the cardinality of both sides of (i) gives:

= (ii)

By proposition 1.3.10, the external potential coupling set of any primary set is disjoint from every other external potential coupling set, thus:

(iii)

Substituting (iii) into (ii) gives:

QED

Proposition 1.3.13

Given an encapsulated set G and given that the i^th primary set is Q_i, the external potential coupling set of Q_i is disjoint from the internal potential coupling set of Q_i, or:

Proof:

By definition [D1.9], the external potential coupling of Q_i is:

= (i)

By definition [D1.8], the internal potential coupling set of Q_i is given by:

= (ii)

Presume thatis not disjoint from. Thus:

(iii)

If (iii) holds, then, given (i) and (ii), there is at least one ordered pair common to bothand,or:

(iv)

But by definition:

(v)

Thus (iv) does not follow and so (iii) is false, or:

(vi)

As Q_i was chosen arbitrarily, we can quantify over all Q_i, thus:

QED

Proposition 1.3.14

Given an encapsulated set G and given that the i^th primary set is Q_i, the external potential coupling set of Q_i is disjoint from the internal potential coupling set of all other primary sets, or:

Proof:

By definition [D1.9], the external potential coupling of Q_i is:

= (i)

Consider any other primary set, Q_j, such that. By definition [D1.8], the internal potential coupling set of Q_j is given by:

= (ii)

Presume thatis not disjoint from. Thus:

(iii)

If (iii) holds, then, given (i) and (ii), there is at least one ordered pair common to bothand,or:

(iv)

But by Proposition 1.3.2. each disjoint primary set is disjoint from every other, or:

(v)

From (v) it follows that there does not exist any element that is a member of both K_i and K_j, or:

Thus (iv) does not follow and so (iii) is false, or:

(vi)

As Q_j in (iii) was considered as any other primary set, we can quantify over all other primary sets, thus:

QED

Proposition 1.3.15

Given an encapsulated set G and given that the i^th primary set is Q_i, all external potential coupling sets are disjoint from all internal potential coupling sets, or:

Proof:

From proposition 3.1.17, the external potential coupling set of Q_i is disjoint from the internal potential coupling set of Q_i, or:

(i)

From proposition 3.1.18, the external potential coupling set of Q_i is disjoint from the internal potential coupling set of all other primary sets, or:

(ii)

From (i) and (ii) it follows that:

QED

Proposition 1.3.16

Given an encapsulated set G of r primary sets, and given that the i^th primary set is Q_i, the potential coupling of Q_i is the sum of the external potential coupling sets of Q_i and the internal potential coupling of Q_i, or:

Proof:

By proposition [D1.10], the potential coupling set of Q_i is given by:

(i)

Taking the cardinality of both sides of (i) gives:

= (ii)

By proposition 1.3.15, all external potential coupling sets are disjoint from all internal potential coupling sets, or:

(iii)

Substituting (iii) into (ii) gives:

QED

Proposition 1.3.17

Given an encapsulated set G of r primary sets, the potential couplingof G is the sum of the internal potential coupling of G and the external potential coupling of G, or:

Proof:

By definition [D1.13], the potential coupling set of G is given by:

(i)

Taking the cardinality of both sides gives of (i) gives:

= (iii)

By definition [D1.11], the internal potential coupling set of G is given by:

(iv)

By definition [D1.12], the external potential coupling set of G is given by:

(v)

Thus from (iv) and (v):

(vi)

From proposition 1.3.15, all external potential coupling sets are disjoint from all internal potential coupling sets, or:

(vii)

Substituting (vii) into (vi) gives:

(viii)

Substituting (viii) into (iii) gives:

QED

Proposition 1.3.18

Given an encapsulated set G of r primary sets and given that the i^th primary set is Q_i, the potential couplingof G is the sum of the internal potential coupling of all Q_i and the external potential coupling of all Q_i, or:

Proof:

By proposition 1.3.17, the potential couplingof G is the sum of the internal potential coupling of G and the external potential coupling of G, or:

(i)

By proposition 1.3.11, the internal potential coupling of G,, is given by:

(ii)

By proposition 1.3.12, the external potential coupling of G,, is given by:

(iii)

Substituting (ii) and (iii) into (i) gives:

=

QED

Proposition 1.3.19

Given an encapsulated set G of r primary sets and given that the i^th primary set is Q_i, the potential couplingof G is the sum of the potential couplings of all Q_i, or:

Proof:

By proposition 1.3.18, the potential couplingof G is the sum of the internal potential coupling of all Q_i and the external potential coupling of all Q_i, or:

(i)

By proposition 1.3.16, the potential coupling of Q_i is the sum of the external potential coupling sets of Q_i and the internal potential coupling of Q_i, or:

(ii)

Substituting (ii) into (i) gives:

QED

Proposition 1.4.

Given an encapsulated set G of r primary sets, of information-hiding violation V and given that the i^th disjoint primary set K_i containselements and has an information-hiding violation of v(K_i), the external potential couplingof Q_i is given by:

Proof:

By definition [D1.9], the external potential coupling set of Q_i is given by:

(i)

Taking the cardinality of (i) gives:

(ii)

As K_i is by definition disjoint from (V \ K_i), then:

= (iii)

By definition [D1.6], the information-hiding violation of K_i is:

(iv)

Substituting (iv) into (iii) gives:

QED

Proposition 1.5.

Given a uniformly-distributed encapsulated set G of n elements and of r primary sets and given that the i^th primary set is Q, the internal potential coupling of Q_i, , is given by:

Proof:

By proposition 1.2:

(i)

By definition, the disjoint primary sets of uniformly-distributed system all contain the average number of elements per disjoint primary set, or:

(ii)

Substituting (ii) in (i) gives:

QED

Proposition 1.6.

Given a uniformly-distributed encapsulated set G of n elements and of r primary sets, the internal potential coupling of G,, is given by:

Proof:

By proposition 1.3.11 the internal potential coupling of G,, is given by:

(i)

By proposition 1.5:

(ii)

Substituting (ii) into (i) gives:

=

=

QED

Proposition 1.7.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, and given that the i^th disjoint primary set K_i has an information-hiding violation of d, the external potential couplingis given by:

Proof:

By proposition 1.3.12, the external potential coupling of set G is given by:

(i)

By proposition 1.4:

(ii)

Substituting (ii) into (i) gives:

(iii)

By the definition of a uniformly-distributed set, the number of elements per disjoint primary set is the same, that is,

(iv)

Substituting (iv) into (iii) gives:

=

=

=

= (v)

By proposition 1.3.6, the sum of the information-hiding violation of all the disjoint primary sets is the cardinality of the information-hiding violational set, or:

(vi)

Substituting (vi) into (v) gives,

(vii)

By definition, d is the information-hiding violation per disjoint primary set,

(viii)

Substituting (viii) into (vii) gives:

=

=

=

QED

Proposition 1.8.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, and given that the i^th disjoint primary set K_i has an information-hiding violation of d, the potential couplingis given by:

Proof:

By proposition 1.3.17, the potential couplingof G is the sum of the internal potential coupling of G and the external potential coupling of G, or:

(i)

By proposition 1.6 the internal potential couplingis given by:

(ii)

By proposition 1.7 the external potential couplingis given by:

(iii)

Substituting (iii) and (ii) into (i) gives:

=

QED

Proposition 1.9.

Given a non-uniformly distributed encapsulated set U of n elements and of r disjoint primary sets, and given that each i^th disjoint primary set K_i contains elements, the sum of the deviations from mean numbers of elements per disjoint primary set is 0.

Proof:

Consider that the elements within set U are not uniformly distributed, but that each disjoint primary set contains elements, where is the mean number of elements per disjoint primary set and z_i is some deviation from that mean, then we can see that:

(i)

By proposition 1.3.6, the sum of the cardinality of all the disjoint primary sets is total number of elements in G, or:

(ii)

Substituting (ii) into (i) gives,

=

And,

QED

Proposition 1.10.

Given an encapsulated set U non-uniformly distributed in hidden elements but uniformly distributed in violational elements, of information-hiding violation V, and given that each i^th disjoint primary set K_i contains elements and has the same information-hiding violation of d, the external potential coupling is independent of distribution of elements within those disjoint primary sets.

Proof:

We shall attempt to prove this Proposition by showing that equation for the external potential coupling of a set whose elements are not uniformly distributed is the same as the equation for the external potential coupling of a set whose elements are uniformly distributed; if the two equations are the same, then the external potential coupling of a set is independent of element distribution.

By proposition 1.7 the external potential coupling,, of a uniformly-distributed encapsulated set G is given by:

(i)

By definition the external potential coupling of the given U is:

(ii)

By proposition 1.3,

(iii)

Substituting (iii) into (ii) gives,

(iv)

Also, given that each disjoint primary set has the same information-hiding violation, d, or:

(v)

Substituting (v) into (iv) gives,

(vi)

If we now consider that the elements within set U are not equally distributed, but that each disjoint primary set contains elements, where is the mean number of elements per disjoint primary set and z_i is some deviation from that mean. Thus,

(vii)

Substituting (vii) into (vii) gives,

As both and d are independent of i, then we can write,

=(viii)

Proposition 1.9 shows that:

(ix)

Substituting (ix) into (viii) gives:

=

= (x)

Even though the information-hidden elements of U are non-uniformly distributed over its disjoint primary sets, each disjoint primary set does have the same information-hiding violation, so by definition:

(xi)

Substituting (xi) into (x) gives:

=

This equation is the same as (i) which governs a system uniformly distributed and therefore the external potential coupling is independent of distribution of elements within those disjoint primary sets.

QED

Proposition 1.11.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d, there does not exist any set, U, not uniformly-distributed in hidden elements, of equal n, r and d, with a lower potential coupling.

Proof:

We shall assume that this Proposition is false and prove that this leads to a contradiction. Thus, consider a set U, not uniformly-distributed, of n elements and r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d; as n, r and d are the same for both G and U, then the sets differ only in how hidden elements are distributed across disjoint primary sets: the hidden elements of G are uniformly distributed, and the hidden elements of U are not uniformly distributed.

Let the i^th primary set of U be J_i. By proposition 1.3.18, the potential coupling of the entire set U is the sum of the internal potential coupling of U and the external potential coupling of U, or:

(i)

If we take the i^th disjoint primary set of G to be Q_i, then by Proposition 1.3.18 again:

(ii)

Assuming that the Proposition's premise is false implies assuming that the potential coupling of G is greater than that of U, or:

(iii)

Substituting (i) and (ii) into (iii) gives,

But as G and U differ only in the distribution of their hidden elements, by Proposition 1.10 their external potential coupling must be equal. Hence,

(iv)

Let M_i be the disjoint primary set of J_i. By proposition 1.2, the internal potential coupling of J_i can be written as:

(v)

Given that U is not uniformly distributed in hidden nodes and thus that the elements within U's disjoint primary sets are not uniformly distributed, we can define that each disjoint primary set contains (a + z_i) elements, where a is defined as the mean number of elements per disjoint primary set and z_i is some deviation from that mean, then:

(vi)

We also note that U's not being uniformly distributed implies that z_i is non-zero for some i, or:

This implies:

(vii)

Substituting (vi) into (v) gives,

(viii)

The internal potential coupling of K_i is also given by Proposition 1.2 as,

(ix)

As G is uniformly distributed, however, then each disjoint primary set contains the same number of elements, a, or:

Substituting this into (ix) gives,

(x)

Substituting into (x) and (viii) into (iv) gives,

(xi)

Proposition 1.9 proves that:

(xii)

Substituting (xii) into (xi) gives,

(xiii)

But (xiii) conflicts with (vii) and thus the initial assumption - that there exists a set, U, not uniformly distributed in hidden nodes, whose potential coupling is lower than that of G - must be false.

QED

Proposition 1.12.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d, the number of disjoint primary sets r_ild that isoledensally minimises the set's potential coupling is given by:

Proof:

By proposition 1.8, the potential coupling of a uniformly-distributed set s_u(G) is given by:

To find the number of disjoint primary sets that isoledensally minimise the potential coupling, differentiate with respect to r and set to zero.

=

= 0

=

=

QED

Proposition 1.13.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d, the number of disjoint primary sets r_h at which point the potential coupling reaches that of an equivalently-ordered unencapsulated set is given by:

Proof:

To find where the potential coupling of G intersects that of the equivalently ordered unencapsulated system, equate the equations of both potential coupling and solve for r.

From proposition 1.1, the equation for the potential coupling of an unencapsulated set is:

(i)

From proposition 1.8, the equation for the potential coupling of a uniformly-distributed set is:

(ii)

Equating (i) and (ii) gives,

=

=

=

If we take the first root,

=

=

r=1

Take second root,

=

QED

Proposition 1.14.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d, the set's minimum isoledensal potential coupling is given by:

Proof:

From proposition 1.8, the potential coupling of a uniformly-distributed set,, is given by:

(i)

From proposition 1.12, the number of disjoint primary sets, r_ild, that minimises the set's potential coupling is given by:

(ii)

Substituting (ii) into (i) gives,

=

=

=

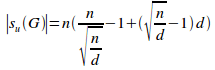
QED

Proposition 1.15.

Given a uniformly-distributed encapsulated set G of n elements and of r disjoint primary sets, and given that the i^th disjoint primary set K_i has an information-hiding violation of d, the number of elements in K_i when the set's potential coupling is isoledensally minimised is given by:

Proof:

As G is evenly distributed then the number of elements in K_i is the average number of elements per disjoint primary set, or:

(i)

From proposition 1.12, the number of disjoint primary sets r_min that minimises the set's potential coupling is given by:

(ii)

Substituting (ii) into (i) gives:

=

=

=

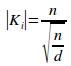
QED

Proposition 1.16.

Given a uniformly-distributed encapsulated set G of n elements, and given that the i^th disjoint primary set K_i has an information-hiding violation of d, the information-hiding violation of K_i when the set's potential coupling is isoledensally minimised is given by:

Proof:

From proposition 1.15, the number of elements in K_i when the set's potential coupling is minimised is given by:

Thus,

QED

REFERENCES

[1] "A critique of cyclomatic complexity as a software metric," Martin Shepperd, 1988.

[2] "On the Criteria To Be Used in Decomposing Systems into Modules," D. L. Parnas, 1972.

[3] "Encapsulation theory fundamentals," Ed Kirwan, www.EdmundKirwan.com/pub/paper1.pdf

[4] "Structured Design," W. Stevens, G. Myers, and L. Constantine, IBM Systems Journal.

[5] Download Fractality: Free Edition (select Tools->Overview), http://www.EdmundKirwan.com/servlet/fractal/GetFrac

[6] http://sourceforge.net/

[7] "The Optimal Class Size for Object-Oriented Software," Khaled El Emam et. al., 2002.

[8] "Module Size Distribution and Defect Density," Yashwant K. Malaiy and Jason Denton.

[9] "A Complexity Measure," Thomas J. McCabe, 1976.

[10] "Information technology - Open Distributed Processing," ISO/IEC 10746, 1998.

[11] "Encapsulation theory: the anomalous minimised configuration," Ed Kirwan, www.EdmundKirwan.com/pub/paper5.pdf