Encapsulation theory: L3 potential coupling.

Edmund Kirwan

www.EdmundKirwan.com ^*

Abstract

This paper establishes that potential coupling exists only for second and third length dependencies. The relationship between both lengths of potential coupling is examined and concludes with the recommendation that, for modification-resilient sets, potential coupling of second length dependencies should be minimised and potential coupling of third length dependencies should be maximised.

Keywords

Encapsulation theory, encapsulation, potential coupling, length.

1. Introduction

In [2] the potential coupling of a primary subset was defined as a subset of the Cartesian product of all the elements of the associated disjoint primary set with themselves and with the elements of violational subset (or rather, the cardinality thereof). This can be used to model, for example, all possible dependencies within a software system whose subsystems correspond to disjoint primary sets and whose violational elements correspond to those program units visible outside their subsystems (and thus towards which dependencies can be formed).

Such a Cartesian product can also be viewed as 2-tuples of the relation R(x, y) where x and y are program units and R is the dependency relation between them, the dependency here being a direct dependency rather than an indirect one. This can be extended, such that the relation R(x, y, z) represents x depends on y which in turn depends on z, or transitively that x indirectly depends on z; and thereafter extended to the limit of the number of elements in the entire encapsulated set, R(e₁, e₂, ..., e_n).

Rather than examining potential coupling in terms of the number of direct dependencies between elements, this paper examines potential coupling in terms of the number of indirect dependencies between elements.

This paper considers encapsulated sets of absolute information-hiding only.

2. Dependencies and lengths

Let us begin by considering actual dependencies, as opposed to potential dependencies. In figure 1, we see eight elements within two disjoint primary sets and a dependency represented as a tuple spanning six elements; the dark elements are violational, the light, information-hidden. As such a dependency is therefore a 6-tuple of the relation R(e₁, e₂, e₃, e₄, e₅, e₆), we shall say that such a dependency is of length six. Let us use the short-hand Lx for a relation of x; the dependency in figure 1 is therefore an L5 dependency.

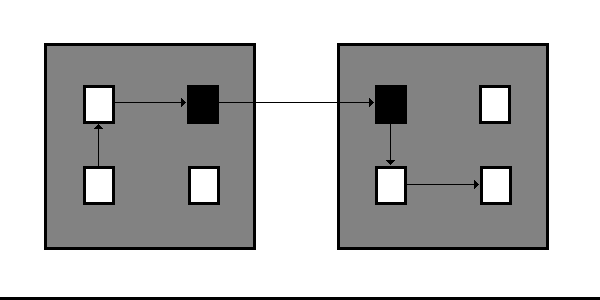
Figure 1: A dependency of five dependencies

We note that the L6 dependency in figure 1 is a simple dependency: we are not interested in counting dependencies on elements from themselves.

When we consider potential coupling, however, the actual tuple in figure 1 becomes just one tuple in a much larger set, potential coupling encompassing all possible, allowable tuples of elements - always respecting information-hiding - between all possible, allowable elements. The question then arises: how long is the shortest dependency between any two elements in an encapsulated set?

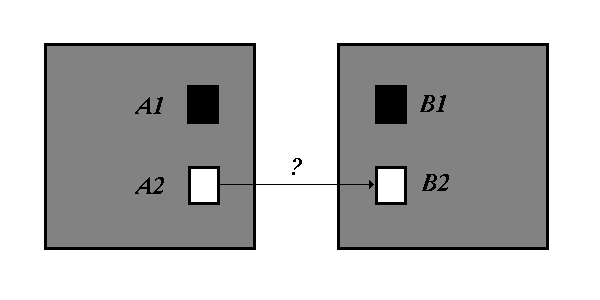
Figure 2: A potential dependency between two information-hidden elements

By definition, an dependency between two elements is a 2-tuple. We can thus say that the potential coupling studied so far is potential coupling of two elements or L2 potential coupling. (Note that, throughout these papers, wherever unqualified potential coupling is mentioned, L2 potential coupling is understood.) Yet L2 potential coupling does not exhaust all possible, unique dependencies within a set. Take figure 2, for example, where again the dark elements are violational, the light, information-hidden. There is clearly a potential L2 dependency between element A2 and B1, as B1 is a violational element and so all other elements may form L2 dependencies towards it.

What about elements A2 and B2? Both these elements are information-hidden within their respective regions and so, by definition, there can be no L2 tuple established comprising both elements. It is possible, however, to join the elements via the L3 tuple (A2, B1, B2). This is a valid 3-tuple, though not one included in the L2 potential coupling. Let us therefore define L3 potential coupling set to be 3-tuples of the relation R(x, y, z) such that the relation R(x, y) and R(y, z) represent the previously-defined L2 potential coupling set.

So is there any L3 or higher potential coupling?

It can be shown that L2 and L3 potential coupling do in fact exhaust all possible shortest dependencies in an encapsulated set (see proposition 6.5); unlike actual dependencies which may be enormously long depending on the size of the set, the maximum length of a shortest dependency in an encapsulated set is three.

This reveals the unpleasant reality that information-hiding exists within an absolute information-hiding context only for L2 dependencies; when L3 are considered, all elements are potentially dependent on all others.

3. The significance of L3 potential coupling

Why investigate L3 potential coupling?

Here we must again step outside encapsulation theory to examine change propagation probability. Let us take a simplistic view of set modification.

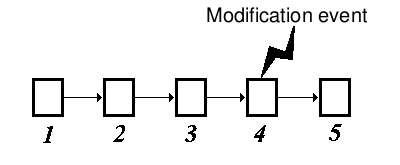
Figure 3: Element 4 undergoes a modification event

Consider a dependency of elements in which any particular element can undergo a, "Modification event." There exists a probability between each element in the dependency that a modification event at one element can cause a modification event at the previous element. This means that a modification event at element x can cause a modification event at element x-1 which can in turn cause a modification event at element x-2, and so on.

Taking this view, it is easy to prove that, given a modification event at element x, the probability of a modification event cannot increase with distance from the modified element (see proposition 6.8). The laws of probability state, in essence, that the modification probabilities must be multiplied with each element traversed from the original, modified element, and as these probabilities are always between 0 and 1 then the probability of ripple modification will usually decrease with each element traversed. Thus in figure 3 a modification event occurs at element 4; it is more probable that this modification event will propagate to element 3 than to element 2, and it is more probable that the modification event will propagate to element 2 than to element 1.

This result should not be overstated. We have discussed neither the nature of the modification nor the nature of probabilistic dependency. In a real-world encapsulated set, such as a computer system, if the modification is as extreme as deleting a program unit, then those dependent program units will definitely be impacted (with a probability of 1). Each program unit further out from the deletion will, however, offer some buffering capability: if program unit B just reads a number from program unit C, then after the deletion of C, B could be updated to hard-code the number, and thus those program units dependent only on B should not be impacted by the deletion of C. A great deal more research on change propagation probability has been done than is presented here (see [5] and [6]).

We can surmise, however, that an encapsulated set of n elements formed predominantly of L2 dependencies will suffer greater from propagated modifications than one formed predominantly of L3 dependencies, which in turn will suffer greater than one formed predominantly from L4 dependencies, etc.

As we have seen, potential coupling comes in only two lengths: L2 and L3. If we wish to design sets resilient to propagated modification, it would seem prudent both to minimise L2 potential coupling and maximise L3 potential coupling.

4. Maximising L3 potential coupling

In [2] we concentrated on minimising L2 potential coupling and found that the number of disjoint primary sets r_ild that isoledensally minimises a uniform encapsulated set's L2 potential coupling is given by:

The question is, then, what number of number of disjoint primary sets isoledensally maximises a uniform set's L3 potential coupling? First we must derive the equation for the L3 potential coupling of a uniform set (see proposition 6.6) and then we must find its maximum (see proposition 6.7). When we do this, we find that the number of disjoint primary sets r_{L3_ild} that isoledensally maximises a uniform set's L3 potential coupling is given by:

As we can see, this is precisely the same as the number of regions that minimise L2 potential coupling; thus when we minimise L2 potential coupling, we maximise L3 potential coupling. This highly desirable state of affairs becomes intuitively appreciable when we consider a law of potential coupling that states that the sum of L2 and L3 potential couplings must be conserved, or (see proposition 6.5):

This implies that when we increase one, we decrease the other, and so when one is minimised, the other must be maximised. Figure 4 shows both L2 and L3 potential coupling as 100 elements are evenly distributed over an increasing number of regions with a specific violation density of 1.

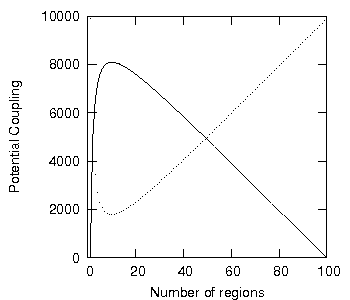
Figure 4: Potential coupling of L2 (points) and L3 (continuous line) potential coupling.

If L3 potential coupling is to be maximised as L2 potential coupling is to be minimised, it is of interest to investigate the ratio of the two, that is, to establish how many potential L3 dependencies can be established for each L2 dependency. It can be shown that such a ratio is calculable for an indefinitely large (in number of elements), uniformly distributed encapsulated set (see proposition 6.12), given the number of regions, r, and hidden density,:

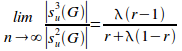
Thus for a uniformly distributed set of 10 disjoint primary sets with a hidden density of 0.75, this equation tells us that for every 1 potential L2 dependency, there are 2 potential L3 dependencies.

For encapsulated sets with a large number of regions, this simplifies to the approximation (see proposition 6.13):

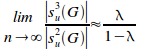
Thus for a large set of hidden density of 0.75, there will be 3 potential L3 dependencies for each potential L2 dependency.

A further variation, finally shows that (see proposition 6.14):

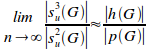
This yet again highlights the benefits in increasing the number of hidden elements and decreasing the number of violational elements. Figure 5 shows a set of the L3/L2 potential coupling ratio as a function of increasing hidden density (as a percentage), given 100 elements uniformly spread over 10 disjoint primary sets, the lesson being: the higher the hidden density, the more potential L3 dependencies there are for every L2 dependency.

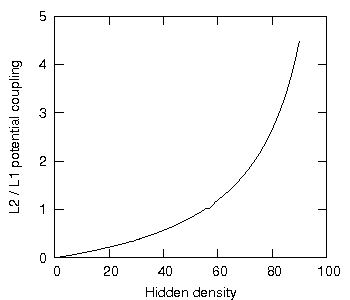
Figure 5: L3 potential coupling divided by L2 potential coupling as a function of increasing hidden density

6. Conclusions

Potential coupling comes in two forms: that with dependencies represented by 2-tuples (L2 potential coupling), and that with dependencies represented by 3-tuples (L3 potential coupling). L2 potential coupling is isoledensally minimised when L3 potential coupling is isoledensally maximised.

7. Author's note

This is an unusual paper in this series, giving prominence to a proposition - proposition 6.8 - which lies outside the scope of encapsulation theory. Although, as mentioned earlier, the proposition should not be over-exaggerated, it nevertheless hints at the core benefit of encapsulation within computer programs.

Given that the probability of a propagated modification event between real program units will usually be less than 1, then the shortest dependency dependencies between program units will be those with the highest probability of propagating a modification event. Thus minimising the number of shortest dependencies (given the isoledensal constraint) also minimises the probability that any modification event will propagate along these maximally-probable dependencies. These shortest dependencies are just the L2 potential coupling, hence the interest in studying L2 potential coupling.

Minimising the overall probability of modification event propagation cannot, however, be the goal of encapsulation (if we put aside qualitative encapsulation for a moment and concentrate on the quantitative). It is clear from proposition 6.8 that such a minimisation is achieved by putting all program units into one subsystem and ensuring that actual dependency dependencies are length-maximised, rendering encapsulation unnecessary.

So what is the benefit of encapsulation? Encapsulation's benefit is in minimising the number of potential dependencies with the highest probability of modification event propagation. It is via this probability management that encapsulation seeks to limit the cost of modification.

Given that a recent survey of open-source Java projects showed the vast majority of systems having a hidden density of just 0.25, L3 potential coupling seems to be a highly squandered resource in modern programming practice.

8. Appendix A

8.1 Definitions

[D6.1] The length of a dependency of x elements is denoted by Lx.

[D6.2] The Lx potential coupling of encapsulated set G, written sⁿ(G), is the number of n-tuples of the relation R(e₁, e₂, ..., e_n) such that the relation R(e_x, e_y) represents the L2 potential coupling set.

8.2 Propositions

Proposition 6.1.

Given an encapsulated set G of r disjoint primary sets and of information-hiding violation, and given that the i^th disjoint primary set K_i containselements and has an information-hiding violation of, the L2 potential coupling of G is given by the equation:

Proof:

By proposition 1.2 in [2], the internal potential couplingis given by:

(i)

By proposition 1.3.11 in [2], the internal potential coupling of set G,, is the sum of the internal potential coupling of Q_i, or:

(ii)

Substituting (ii) into (i) gives:

(iii)

By proposition 1.4 in [2], the external potential couplingof Q_i is given by:

(iv)

By proposition 1.3.12 in [2], the external potential coupling of set G,, is the sum of the external potential coupling of Q_i, or:

(v)

Substituting (v) into (iv) gives:

(vi)

By proposition 1.3.17 in [2], the potential coupling of set G, written, is the sum of the internal and external potential coupling of G, or:

(vii)

Substituting (iii) and (vi) into (vii) gives.

=

QED

Proposition 6.2.

xxx Need to completely re-write this proposition ...

Given a set G of r disjoint primary sets, of information-hidingand given that the i^th disjoint primary set K_i containselements and has an information-hiding of, the number of external elements, x, towards which K_i may direct L3 dependencies towards is given by:

x =

Proof:

By definition, the number of elements external to K_i is the sum of the numbers of elements in all disjoint primary sets except K_i, or:

num. elements external to K_i =

But elements in K_i may not form L3 dependencies towards all these other elements, as some may be information violational; K_i may only form L3 dependencies towards information-hiding elements.

By definition, the x we seek is the number of information-hiding elements external to K_i, which is the sum of the numbers of information-hiding elements in all disjoint primary sets except K_i, or:

By definition, the information-hiding of the entire set,, is the sum of the information-hiding of all its disjoint primary sets:

=

If we consider the i^th disjoint primary set K_i in this sequence, we can write:

=

And thus,

=

But,

= = x

Therefore,

x =

QED

Proposition 6.3.

Given an encapsulated set G of r disjoint primary sets and of information-hiding, and given that the i^th disjoint primary set K_i containselements and has an information-hiding of, the L3 potential coupling of Q_i is given by the equation:

Proof:

By definition, the L3 potential coupling of a disjoint primary set is the number of L3 dependencies formed out of that disjoint primary set towards the information-hidden elements of all other disjoint primary sets.

The number of L3 dependencies formable out of disjoint primary set K_i is the number of tails (elements within K_i) multiplied by the number of external heads (information-hidden elements towards which K_i may direct L3 dependencies).

But K_i containselements and by proposition 6.2 the number of external elements towards which K_i may direct L3 dependencies is given by:

Therefore the L3 potential coupling s³(K_i) of K_i is given by:

QED

Proposition 6.4.

Given an encapsulated set G of r disjoint primary sets and of information-hiding, and given that the i^th disjoint primary set K_i containselements and has an information-hiding of, the L3 potential coupling of G is given by the equation:

Proof:

By proposition 1.3.19 in [2], the L3 potential coupling of set G is the sum of the L3 potential coupling of all its primary sets, or:

(i)

By proposition 6.3, the L3 potential coupling of K_i is given by the equation:

(ii)

Substituting (ii) into (i) gives (i) gives:

QED

Proposition 6.5.

Given an encapsulated set G of r disjoint primary sets with an information-hiding ofand an information-hiding violation of, and given that the i^th disjoint primary set K_i containselements and has an information-hiding ofand an information-hiding violation of, the L2 and L3 potential couplings of G combined exhaust all possible potential coupling dependencies in G.

Proof:

By proposition 1.1 of [2], the maximum possible number of dependencies between the n elements of an unencapsulated set is given by:

(i)

By definition, all Lx dependencies (where x > 1) are composed of x L2 dependencies. Therefore (i) represents the maximum possible number of dependencies in any set G.

By proposition 6.1, the L2 potential coupling of G is given by the equation:

(ii)

By proposition 6.4, the L3 potential coupling of G is given by the equation:

(iii)

Adding (ii) and (iii) gives:

= (iv)

By definitions [D3.6] in [4], xxx need to revisit this:

(v)

(vi)

Substituting (v) and (vi) into ((iv) gives:

= (vii)

By proposition 1.3.5 in [2], the order of G is the sum of the orders of K_i or:

(viii)

Substituting (viii) into (vii) gives:

This is the same as the maximum number of dependencies in G given by (i) so the L2 and L3 potential couplings of G combined exhaust all possible potential coupling dependencies in G.

QED

Proposition 6.6.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, with an information-hiding violation ofand given that the i^th disjoint primary set K_i has an information-hiding violation of d, the L3 potential couplingis given by:

Proof:

By proposition 6.4, the L3 potential coupling of G is given by the equation:

(i)

By definition [D3.6] in [4],

(ii)

By definition [D1.14] in [2],

(iii)

(iv)

(v)

Substituting (iii) and (iv) into (ii) gives:

(vi)

Also by definition [D3.6] in [4],

(vii)

Substituting (v) into (vii) gives:

(viii)

Substituting (vi) and (viii) into (i) gives:

= (ix)

By proposition 1.3.5 in [2], the order of G is the sum of the orders of K_i or:

(x)

Substituting (x) into (ix) gives:

QED

Proposition 6.7.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d, the number of disjoint primary sets r_ild that maximises the set's L3 potential coupling is given by:

Proof:

By proposition 6.6, the L3 potential couplingof a uniformly distributed set is given by:

To find the number of disjoint primary sets that maximise the L3 potential coupling, differentiate with respect to r and set to zero:

=

=

=

QED

Proposition 6.8.

Given a dependency of j elements, A_j, and given that q>m, the probability that a modification event at element k will cause a modification event at element k-m is greater than or equal to the probability that the event at element k will cause a modification event at element k-q.

Proof:

Let A_j be a dependency of j elements.

Let E_j be a modification event at element j.

Let the probability exist that modification event E_j causes modification event E_j-1 such that if E_j-1 is completely independent of E_j then this probability is 0 and if E_j-1 is completely dependent on E_j then this probability is 1, all values in-between signifying partial dependence. Let this probability that event E_j causes event E_j-1 be denoted by P(E_j-1).

Let k, q and m be such that m < q < k < j.

Consider modification event E_k.

The probability that this event will cause event E_k-1 is by definition P(E_k-1).

The probability that event E_k-1 will then cause further event E_k-2 is conditional upon whether event E_k-1 actually takes place. By the rules of conditional probability, the probability that both E_k-1 and E_k-2 take place is given by:

Whereis the probability that event E_k-2 occurs given that event E_k-1 occurred. This is also a number between 0 and 1.

Similarly, the probability of E_k-3 is given by:

(i)

Letbe the conditional probability P(E_k-x | E_k-1 and E_k-2 and … and E_k-x+1). Thus we can re-write (i) as:

And in general we can write:

Consider the two cases m and q:

(ii)

(iii)

As m < q let us define:

(iv)

Substituting (iv) into (iii) gives:

(v)

Dividing (ii) by (v) gives:

=

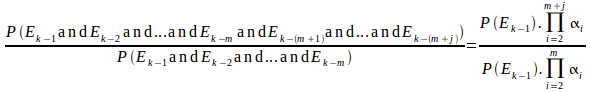
Asthen

(vi)

Thus (vi) proves that the probability that a modification even at element k will propagate to element k-q is less than or equal to the probability that the event will propagate to element k-m.

Thus the probability that a modification event at element k will cause a modification event at element k-m is greater than or equal to the probability that the event at element k will cause a modification event at element k-q.

QED

Proposition 6.9.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, and of information-hiding density of, the specific information-hiding violation, d, is given by:

Proof:

By definition [D1.14] in [2]:

(i)

By definition [D3.6] in [4],

(ii)

By definition [D5.3] in [3],

(iii)

Substituting (iii) into (ii) gives:

(iv)

Substituting (iv) into (i) gives:

=

QED

Proposition 6.10.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, and of information-hiding density of, the L3 potential couplingis given by:

Proof:

By proposition 6.6, the L3 potential couplingis given by:

(i)

By proposition 6.9, the specific information-hiding violation, d, is given by:

(ii)

Substituting (ii) into (i) gives:

=

=

=

=

QED

Proposition 6.11.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, and of information-hiding density of, the L2 potential couplingis given by:

Proof:

By proposition 1.8 in [2]:

= (i)

By proposition 6.9, the specific information-hiding violation, d, is given by:

(ii)

Substituting (ii) into (i) gives:

=

QED

Proposition 6.12.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, and of information-hiding density of, the limit of the ratio of L3 potential coupling to L2 potential coupling as the set grows indefinitely large is given by:

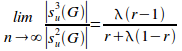
Proof:

By proposition 6.10, the L3 potential couplingis given by:

(i)

By proposition 6.11, the L2 potential couplingis given by:

(ii)

Dividing (i) by (ii) gives:

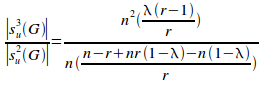
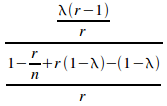= (iii)

Taking the limit of (iii) as n tends to infinity gives:

=

=

=

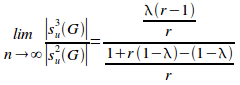
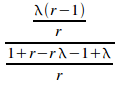
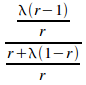
QED

Proposition 6.13.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, and of information-hiding density of, the limit of the ratio of L3 potential coupling to L2 potential coupling as the set grows indefinitely large, given a large number of disjoint primary sets, is given by:

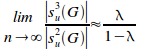
Proof:

By proposition 6.12, the limit of the ratio of L3 potential coupling to L2 potential coupling as the set grows indefinitely large is given by:

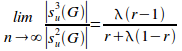(i)

Ifthen:

(ii)

Substituting (ii) into (i) gives:

=

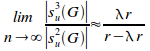
QED

Proposition 6.14.

Given a uniformly distributed encapsulated set G of n elements and of r disjoint primary sets, and of information-hiding density of, the limit of the ratio of L3 potential coupling to L2 potential coupling as the set grows indefinitely large, given a large number of disjoint primary sets, is given by:

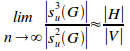
Proof:

By proposition 6.13, the limit of the ratio of L3 potential coupling to L2 potential coupling as the set grows indefinitely large, given a large number of disjoint primary sets, is given by:

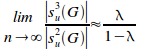(i)

By definition [D5.3] in [3]:

(ii)

By definition [D3.6] in [4],

(iii)

Dividing (iii) by n gives:

(iv)

Substituting (ii) into (iv) gives:

(v)

Substituting (ii) and (v) into (i) gives:

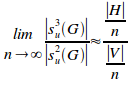
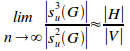
QED

9. References

[1] "Encapsulation theory: L3 potential coupling," Ed Kirwan, www.EdmundKirwan.com/pub/paper6.pdf

[2] "Encapsulation theory fundamentals," Ed Kirwan, www.EdmundKirwan.com/pub/paper1.pdf

[3] "Encapsulation theory: the anomalous minimised configuration," Ed Kirwan, www.EdmundKirwan.com/pub/paper5.pdf

[4] "Encapsulation theory: the transformation equations of absolute information-hiding," Ed Kirwan, www.EdmundKirwan.com/pub/paper3.pdf

[5] "Change Prediction in Object-Oriented Software Systems: A Probabilistic Approach," Ali R. Sharafat and Ladan Tahvildari.

[6] "Predicting the Probability of Change in Object-Oriented Systems," Nikolaos Tsantalis, Alexander Chatzigeorgiou and George Stephanides.