
Maximum information.
What configuration maximizes a system's information?
This is a short aside from the first information post here.
Given that information in some sense measures the degree of selectability with which methods depend on other methods, we might expect that systems display greatest information when each method depends maximally on all others. This turns out to be the case, practicality notwithstanding. Let us consider first five methods and connect them such that they maximally depend on one another with the caveat that we shall disallow circular dependencies (we are civilized programmers after all). See figure 1.
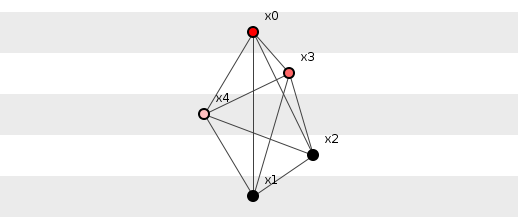
Figure 1: Five methods configured for maximum information.
Figure 1 shows method x0() at the top depending on all others below. Next, method x3() depends on all others except on x0() (which would be a circular dependency). x4() depends on all other methods except x0() and x3(), etc.
Calculating the information of this structure shows it to have 14.8 bits of information, divided among the methods as:
- Info. of
x0() = 0 bits. - Info. of
x3()=log2(4) = 2 bits. - Info. of
x4()=log2(4) + log2(3) = 3.58 bits. - Info. of
x2()=log2(4) + log2(3) + log2(2) = 4.58 bits. - Info. of
x1()=log2(4) + log2(3) + log2(2) + log2(1) = 4.58 bits.
For example, method x3() has one parent, x0(), with four children, so x3()'s peer set is four so its information is log2(4). x4(), however, has two parents: x0() and x3(); its peer set from x0() has four elements and its peer set from x3() has three elements, so its information is log2(4) + log2(3), and so on.
If we maximally configure the next system up, that of six methods, we find a similar cat's cradle, as shown in figure 2.

Figure 2: Six methods configured for maximum information.
This second system has an information of 26.4 bits with the contributions from individual methods shown below:
- Info. of
x0() = 0 bits. - Info. of
x3()=log2(5) = 2.32 bits. - Info. of
x4()=log2(5) + log2(4) = 4.32 bits. - Info. of
x5()=log2(5) + log2(4) + log2(3) = 5.91 bits. - Info. of
x2()=log2(5) + log2(4) + log2(3) + log2(2) = 6.91 bits. - Info. of
x1()=log2(5) + log2(4) + log2(3) + log2(2) + log2(1) = 6.91 bits.
A pattern emerges, with the maximum information of any collection of n elements connected without circular dependencies being given by the equation:
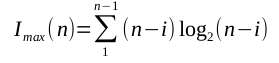
For typical software systems, however, this equation yields astronomical values, far exceeding realistic expectation. Spring's core functionality, for instance, with its 4500 methods, has a maximum information content of more than one hundred million bits, yet that program's actual information barely creeps above 36,000 bits, a disparity whose vastness reflects both the unreasonable nature of maximal connectivity and the inappropriateness of maximum information as a design heuristic.