
Notes: the ripple hypothesis.
This topic was tackled before, but only qualitatively. Hence this more quantitative approach.
How to we measure these probabilities?
According to the classical definition of probability, all we need to measure the probability of method m's changing is to measure the ratio of the number of times m actually changes to the number of revisions in the limit as the numbers of changes and revisions approach infinity. Few programs on github, however, have yet reached an infinite number of revisions, so we'll make an approximation: the probability that m changes is the large number of times it changes during a large number of revisions divided by that number of revisions. This is why we need to analyze large numbers of changes and large numbers of consecutive revisions.
Given this, we can calculate the conditional probability:
| P(δ(m) ∩ δ(Cm)) | |
| P(δ(m) | δ(Cm)) = |
|
| P(δ(Cm)) |
P(δ(m) ∩ δ(Cm)) is the number of revisions in which method m changes simultaneously with any one of its children (divided by the total number of revisions). P(δ(Cm)) is the total number of times than any child of m changes (divided by the total number of revisions).
Let's take the example shown in figure 3, in which a program of just 3 methods evolves over 4 revisions, where the amateurish, un-anti-aliased, irregular blue "circles" indicate code update to a method.
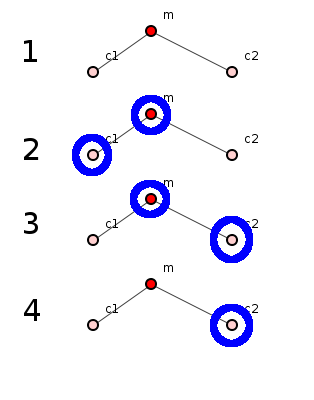
Figure 3: A system of 3 methods evolving over 4 revisions.
All 3 methods are created in revision 1; this is not considered a change. In revision 2, both m and c1 change. In revision 3, both m and c2 change. In revision 4, only c2 changes.
Let's calculate the change probabilities of each method.
The probability of a change in method m given a change to any child is 2/3 because it changes twice simultaneously with any of its children's changes, and the number of revisions in which any child changes is 3. The probability of a change in m given a change to any antecedent is 0 because it has no antecedents.
The probability of a change in method c1 given a change to any of its children is 0 because it has no children. The probability of a change in c1 given a change to any of its antecedents is 1/2 because it changes only once simultaneously with its antecedent, and that antecedent changes a total of 2 times.
Method c2 has the same probabilities as c1.
The system's ripple bias is the sum of all child-related probabilities divided by the sum of all antecedent-related probabilities. So the ripple bias for this system is: (2/3) / (1/2 + 1/2) = 2/3.
The Java programs were taken randomly from github, though certain criteria had to be met. The programs had to be non-trivial (with more than 1000 methods) and had to have enough commits for the program to have evolved at least 1000 method changes. The programs also had to be easy to compile: if it didn't compile with ant, maven or gradle, it was dismissed with unimaginable revulsion.
Spoklin Soice analyzed the programs and produced raw data which was then fed into a grotesque parser poorly written by the author to calculate the ripple bias.
| Program | #Revs | #Changes | #LOC | CDR | Child corr. | Ante. corr. | Ripple bias |
| ant | 1504 | 1975 | 4812610 | 1.85 | 0.41 | 0.05 | 1.36 |
| atmosphere | 1149 | 3834 | 4679350 | 1.36 | 0.52 | 0.06 | 1.12 |
| bitcoinj | 596 | 1652 | 3547778 | 1.92 | 0.36 | 0.03 | 0.97 |
| commafeed | 1294 | 1933 | 604825 | 2.81 | 0.33 | 0.07 | 1.21 |
| gitblit | 1890 | 2906 | 10779729 | 4.63 | 0.44 | -0.19 | 2.08 |
| jackson | 1598 | 4104 | 4985775 | 2.77 | 0.35 | 0.03 | 1.1 |
| java-dvr | 353 | 5695 | 613573 | 1.24 | 0.04 | 0 | 1.3 |
| jedis | 1222 | 7371 | 1331930 | 1.4 | 0.17 | 0.18 | 1.95 |
| jsoup | 499 | 3445 | 628246 | 0.76 | -0.06 | 0.06 | 1.32 |
| mapdb | 1946 | 8441 | 4506846 | 2 | 0.3 | 0.04 | 1.37 |
| mina | 780 | 1533 | 2075634 | 1.21 | 0.32 | 0.03 | 1.47 |
| mockito | 1432 | 1874 | 768854 | 1.52 | 0.18 | 0.02 | 1.52 |
| nutch | 468 | 1152 | 1126970 | 1.01 | 0.26 | -0.01 | 0.93 |
| OpenGrok | 634 | 2515 | 3086448 | 2.46 | 0.31 | 0.05 | 1.75 |
| RxJava | 1357 | 9465 | 7009369 | 2.82 | 0.08 | 0.07 | 1.65 |
| scouter | 1543 | 1076 | 4436123 | 1.48 | 0.19 | 0.13 | 1.05 |
| sonatype | 1028 | 2128 | 1543476 | 1 | 0.4 | -0.08 | 1.08 |
| swagger | 1181 | 4143 | 2816018 | 0.7 | 0.2 | -0.04 | 0.98 |
| traccar | 651 | 2652 | 1369662 | 3.48 | 0.51 | -0.53 | 3.3 |
| traccar | 1550 | 3201 | 3686489 | 1.98 | 0.36 | -0.14 | 2.58 |
| Total | 22675 | 71095 | 64409705 | 38.38 | 5.67 | -0.15 | 30.09 |
| Average | 1133.75 | 3554.75 | 3220485.25 | 1.92 | 0.28 | -0.01 | 1.5 |
Table 1: Data over all revisions.
In the table above, the columns are as follows:
- #Revs: number of consecutive revisions analyzed.
- #Changes: number of changed methods found throughout the series of revisions.
- #LOC: the approximate number of lines of source code analyzed (it was found that, loosely, one line of source code produces 49 bytes of bytecode, so this figure is just the number of bytes analyzed divided by 49).
- CDR: the change density ratio, that is, the ratio of the number of changes per line of code in dependent methods, divided by the number of changes per line of code in independent methods.
- Child corr.: the correlation between the number of changes a changed method undergoes and the number of methods it depends on.
- Ante. corr.: the correlation between the number of changes a changed method undergoes and the number of methods that depend on it.
- Ripple bias: the ratio of the probability of change in a method given a change in the methods it depends on, to the probability of change in a method given a change in any method that depends on it.
To keep analysis times reasonable (processing a program over its lifetime can easily take 24 hours), programs were not analyzed in their entirety: usually only part of the program was analyzed (so long as the part had > 1000 methods). Also, as bytecode was analyzed, the analysis divided program histories into series compiled with the same version of Java, so as to avoid false-positive changes stemming from merely moving to a newer JVM at some point in the program's lifetime. Traccar appears twice as it happens that two ranges of its consecutive updates, each on a different Java version, met the criteria (>1000 method changes) to earn it double candidacy.
This is probably a lower bound.
If we have two methods, a() and b(), where a() depends solely on b() and b() is depended-on solely by a(), then a change analysis may identify that both methods change in a particular revision, but no algorithm can decide whether the change was made to a() and then rippled down to b(), or the change was made to b() and rippled up to a(). It is entirely symmetrical. The only way to answer this would be to ask the original programmer, and ... just no.
Ripple bias can only expose itself where a() has multiple children or antecedents.
Yet there is little reason to suppose that ripple effects behave differently in single-dependency cases than multiple. Given that the ripple bias is clearly non-unity, then perhaps interviews with all those programmers would also reveal that ripple effects go from depended-on to depended-from in single-dependency cases and that the ripple bias is actually higher than we can determine with algorithm alone.
Of course, this post is just an idea and threats to validity are legion.
One particular difficulty lies in how this analysis identifies change: by measuring bycode. Abstract and interface methods have no bytecode, so this analysis detect changes only in concrete methods.
A common way that an interface method, say, might change is that a new argument is added to its method signature, so a(String) might change to a(String, int). It is, however, impossible for an algorithm to distinguish such a change from the introduction of a new method that just happens to have the same name but a different argument list.
We could simply make that assumption: that all (unique) methods distinguished by class-name and method-name are the same method across revisions if differing only by argument list, and indeed such an attempt was made in the early life of the parser used, but it felt a little ... uncertain.
Perhaps capturing interface changes deserves more attention. Again, however, there is little reason to presume that ripple effects behave different for interface methods than concrete, so including interface changes may increase ripple bias further.
An on unrelated point, it's not even certain that expressing the ripple bias as a ratio is a better description of events than, say, expressing it as the subtraction: P(δ(m) | δ(Cm)) - P(δ(m) | δ(Am)). Some configurations of changes can occur where small numbers of antecedent changes can flatter the ripple bias as the antecedent changes appear in the denominator; these would surely not be present in the subtractive form. More analysis is required, though note that, whatever proves to be the best way to measure ripple effects, data show that dependent methods change almost twice as often as independent methods and this motivates the structural imperative of the post as much as any theoretical framework.
Just for information, if we drop the requirement for analyzed programs to generate 1000 changed methods and allow series with merely 200 changed methods, then we get the table below, with the average ripple bias falling to 1.35, though the CDR stays relatively unchanged at 1.93.
| Program | #Revs | #Changes | #LOC | CDR | Child corr. | Ante. corr. | Ripple bias |
| Aeron | 285 | 379 | 373366 | 1.19 | 0.22 | -0.14 | 0.77 |
| ant | 1504 | 1975 | 4812610 | 1.85 | 0.41 | 0.05 | 1.36 |
| atmosphere | 1149 | 3834 | 4679350 | 1.36 | 0.52 | 0.06 | 1.12 |
| bitcoinj | 596 | 1652 | 3547778 | 1.92 | 0.36 | 0.03 | 0.97 |
| commafeed | 1294 | 1933 | 604825 | 2.81 | 0.33 | 0.07 | 1.21 |
| commons | 261 | 480 | 780177 | 0.49 | 0.37 | 0 | 0.99 |
| commons | 403 | 266 | 1219548 | 0.77 | -0.14 | -0.2 | 1.09 |
| gitblit | 1890 | 2906 | 10779729 | 4.63 | 0.44 | -0.19 | 2.08 |
| jackson | 1598 | 4104 | 4985775 | 2.77 | 0.35 | 0.03 | 1.1 |
| java | 353 | 5695 | 613573 | 1.24 | 0.04 | 0 | 1.3 |
| jedis | 1222 | 7371 | 1331930 | 1.4 | 0.17 | 0.18 | 1.95 |
| jsoup | 499 | 3445 | 628246 | 0.76 | -0.06 | 0.06 | 1.32 |
| logstash | 269 | 223 | 228332 | 4.7 | 0.35 | 0.24 | 1.34 |
| mapdb | 1946 | 8441 | 4506846 | 2 | 0.3 | 0.04 | 1.37 |
| mina | 780 | 1533 | 2075634 | 1.21 | 0.32 | 0.03 | 1.47 |
| mockito | 1432 | 1874 | 768854 | 1.52 | 0.18 | 0.02 | 1.52 |
| nutch | 300 | 537 | 532338 | 2.25 | 0.31 | -0.03 | 0.8 |
| nutch | 468 | 1152 | 1126970 | 1.01 | 0.26 | -0.01 | 0.93 |
| nutch | 542 | 713 | 1170171 | 1.05 | 0.31 | 0.01 | 0.9 |
| OpenGrok | 577 | 239 | 2299176 | 3.85 | 0.16 | 0.58 | 0.9 |
| OpenGrok | 634 | 2515 | 3086448 | 2.46 | 0.31 | 0.05 | 1.75 |
| RxJava | 1357 | 9465 | 7009369 | 2.82 | 0.08 | 0.07 | 1.65 |
| scouter | 1543 | 1076 | 4436123 | 1.48 | 0.19 | 0.13 | 1.05 |
| sonatype | 1028 | 2128 | 1543476 | 1 | 0.4 | -0.08 | 1.08 |
| spring | 412 | 226 | 1556514 | 1.41 | 0.11 | -0.09 | 0.92 |
| swagger | 1181 | 4143 | 2816018 | 0.7 | 0.2 | -0.04 | 0.98 |
| traccar | 651 | 2652 | 1369662 | 3.48 | 0.51 | -0.53 | 3.3 |
| traccar | 1550 | 3201 | 3686489 | 1.98 | 0.36 | -0.14 | 2.58 |
| Total | 25724 | 74158 | 72569327 | 54.07 | 7.36 | 0.22 | 37.79 |
| Average | 918.71 | 2648.5 | 2591761.68 | 1.93 | 0.26 | 0.01 | 1.35 |