
How many classes and packages
should you have?
Real world experience.
Once upon a time there lived a family of programming bears.
Each morning mammy bear, daddy bear and baby bear would rise and eat breakfast together in their secluded cottage deep in the forest before whipping out their three laptops to spend hours cheerily writing Java code.
One day, while the bears were out shopping, professor of automation theory and software engineering, Maria G. Locks, stumbled upon the cottage while lost in the woods. Cupping her hands against the glass as she peered through a window she spied the glowing screens of three laptops and immediately smashed her way inside.
She sat at the first laptop, cracked its password and pored over the Java source code. It was a frightful mess. With just a few, monstrous classes containing thousand-line-long functions, the structure gashed her soul. Distraught, she moved to the second laptop and cracked its password. A rancid splurge of code vomited itself up onto the screen, this time with hundreds of fiddly packages hosting hundreds of tiny classes, each in turn baring masses of disjointed functions. Cracking a final password she sank weeping before the third laptop.
This code was beautiful.
The packages were neither too big nor too small, neither too many nor too few. The well-proportioned classes housed coherent implementation detail. The functions, appropriately information-hidden, performed single tasks without fuss.
Then the three bears burst in through the front door and daddy bear roared with murderous rage at the sight of the intruder. Professor Locks, screaming, leaped to her feet. Mammy bear shrieked something about porridge and a bed but no one could really remember how the tale ended so the whole thing was just abandoned.
The point being?
When is our software neither over-encapsulated, with too many packages and classes, nor under-encapsulated, with too few? When is it just right?
Let us try to answer these questions by modeling a Java program.
Novices often ask, "How many classes should you have?" Though unaware of their omission, they are actually asking, "How many classes should I have to satisfy a particular constraint?" We, too, must choose our constraint. Real-world constraints usually relate to the problem-domain but, wishing our model to be as widely-applicable as it is simple, we shall choose as our constraint that we want to minimize the number of potential dependencies that our system can support. That is, we wish to minimize the system's potential coupling.
Though simple, our choice is not without merit, for we wish (deep breath) to minimize the cost of developing our software and that means minimizing ripple-effect updates by minimizing the number of dependencies involved and that means minimizing the conditions that encourage dependency-formation and that means minimizing the number of potential dependencies.
Eyebrows no doubt rise at such rattling chains of logic but the prize - that of an objective measure of how many functions, classes and packages we should have - might be worth some leeway.
Model assumptions.
Our model is based on two assumptions: one sensible, one completely bonkers.
The first assumption is that our system consists of n functions. Our task is find the number classes and packages over which we should distribute these n functions so that we minimize the potential coupling.
The second assumption is that all functions will be evenly distributed over all classes and packages, that each class will have d functions visible to other classes in the package and that each package will have the same number, d, functions visible to other classes in other packages.
See? Bonkers.
But not without a smidgen of rationale. We know that evenly-distributing functions minimizes potential coupling in almost all cases. Because potential coupling rises with the square of number of elements that can see one another, if a class has twice as many functions then it will have four times as much potential coupling.
As for having a strict number of default-accessor functions per class and public functions per package, well, precisely no one designs a system that way. Programmers try, though, to minimize the number of maximally-visible elements so we can look at d = 1 as an ideal if asymptotic goal. Certainly once a system is up and running it must have an average number of default-accessor functions per class and public functions per package. Given that we want both numbers to be small it is perhaps not so outlandish to find that they might be similar.
Our assumptions, however, these are. Judge their plausibility for yourself.
Finally, let us label our quarry: we wish to know how many packages, pa, and classes, r, our system should have.
So, how do we find pa and r?
What a function sees.
Let us take any function - we shall call it test1() - in our hypothetical, evenly-distributed system and ask: how many other functions can test1() see? Everything here follows from this question.
There are three groups of functions that test1() can see. It can see functions within its own class. It can see functions in other classes within its own package. And it can see functions in other classes in other packages.
These three groups, taken together, comprise all the functions visible to test1(), that is, they give the potential coupling of test1(). For reasons that will become clear, we wish to find an equation for this potential coupling. To do this we must find three terms, one corresponding to each of these three groups.
Functions in own class.
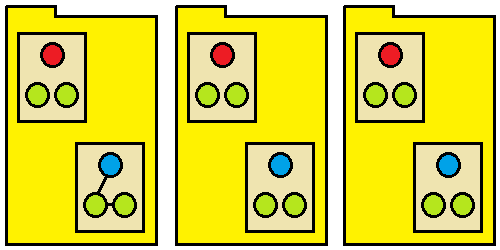
Figure 1: Potential dependencies from test1() within the own class.
Figure 1 shows three packages, each with two classes, each class housing three functions. The red functions are public (their classes are also public), the green private and default-accessor functions are blue. Our test1() function is selected at random to be the one in the bottom-left, as indicated throughout.
How many functions can test1() see in its own class?
Well, it can see all of them; in the example above it can see both other functions in its class. We know that the number of functions in any class is just the total number of functions, n, divided by the total number of classes, r, so we might think that the number is n / r. But this would also include a dependency from test1() on itself, which we would like to ignore, thus the number of dependencies that can form is one less than the number of functions in the class, that is:
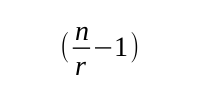
Functions in own package.
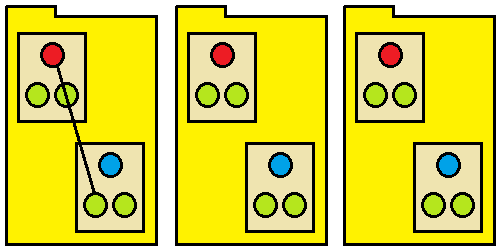
Figure 2: Potential dependencies from test1() within the own package.
How many functions can test1() see in other classes within its own package?
It can see those functions that are not private in all other classes in the package; in the example above it can see just one other public function. We know that the number of functions that are not private in each class is d by definition. And we know that the number of classes per package is just the total number of classes, r, divided by the number of packages, pa, though, again, we wish to exclude to possibility of test1()'s forming dependencies on its own class. So the number of functions it can see in its own package is:
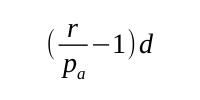
Functions in other packages.
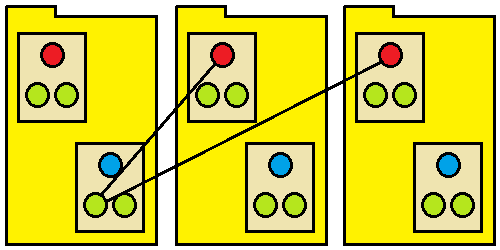
Figure 3: Potential dependencies from test1() towards other packages.
How many functions can test1() see in other packages?
It can see all public functions in all public classes in all other packages; the example above shows it forming dependencies on two other public functions. We know that the number of packages is pa and the number of public functions per package is d by definition. Again, we shall discount forming dependencies within its own package, so the number of functions it can see in other packages is:
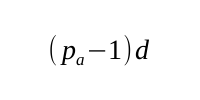
These are the three terms that make up the potential coupling of our one function. To find the potential coupling of the entire system we just multiply them by the total number of functions, n, to give our final equation for the potential coupling, s:
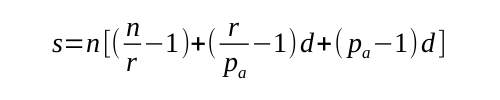
Now, it is well-known that the greatest complaint raised by students learning Java is that there are too few partial differential equations.
It so happens that our quest to find the number of classes and packages to minimize potential coupling involves just such beasts: for we face an optimization problem. Remember those from high-school? Set the derivative to zero and solve? That's all we need to do now, thank you, Mister Newton ... erh, Herr Leibniz ... whatever.
To find the number of classes, r, that minimizes the potential coupling, s, we calculate the derivative of s with respect to r:
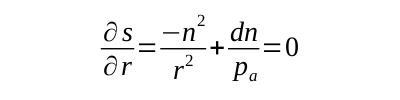
To find the number of packages, pa, that minimizes the potential coupling, s, we calculate the derivative of s with respect to pa:
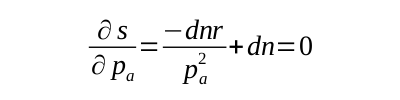
Solving both simultaneous equations gives solutions:
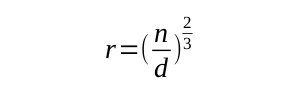
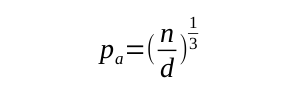
Thus if you have a system of 400 functions, that is n = 400, and aim to have 5 functions per class visible within a package, that is d = 5, then the number of packages you should have is 4, each with 18 classes.
Figure 4 plots our model's potential coupling of 400 functions over all possible of numbers of packages, on the x-axis, and numbers of classes, on the y-axis, with each coordinate coloured red in proportion to the amount of potential coupling generated by that combination of package and class number; thus light pink implies wonderfully-low potential coupling. (The graph is triangular as we cannot have fewer classes than non-empty packages.) The black square indicates the potential coupling minimum.
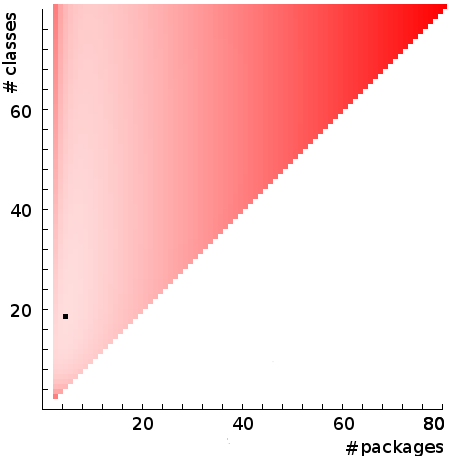
Figure 4: Potential coupling of 400 functions as a function of package and class number, with d=5.
Of course, you would never create such a system. Having only 4 packages for so many functions strikes as far too few; brutal reality would surely barge in and dictate 8 packages, or 10.
This is where the efficiency* of your system comes into play.
100%-efficient systems are as rare as 100%-efficient steam engines. You should gladly descend to 80% or 70% efficiency to win some elbow-room for your design, to enjoy more semantically-driven packages and less-regular distributions than the restrictive ideal case demands. But you may hesitate to fall to the crass encapsulation of only 40% or 30% efficiency, opening your system to the possibility of enormous numbers of dependencies and their subsequent ripple-effect costs.
Infra-red-goggles time.
Figure 5 shows an efficiency heat-map of our 400 functions generated by the same potential coupling equation derived above. The dark-blue area shows efficiency of above 90%, a tropical island untrodden by human feet. The cyan, green and yellow bands offer configurations of a more reasonable trade-off between practicality and potential expense. The red area, well ...
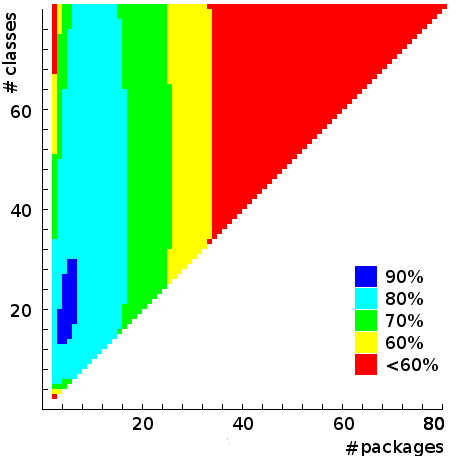
Figure 5: Absolute ideal efficiency of 400 functions as a function of package and class number, with d=5.
Summary.
How many classes and packages should you have?
Altogether now, "It depends."
It depends in particular on the constraint you choose to satisfy. The constraint chosen here was that which tries to minimize development cost by minimizing potential ripple-effect updates.
A simple model was built on some dubious assumptions which lead to some perhaps interesting conclusions.The model can easily be extended, at the cost of complexity, to more-accurately capture reality though, in the end, the model itself has perhaps less to offer than the method by which it was conceived.
However many classes and packages you decide to have, at least be aware of the principles by which you make your decisions.
The only bad design is no design.
Photo credit attribution.
CC image Goldilocks and the Three Bears courtesy of GettysGirl4260 on Flickr.
CC image The front window in the kitchen courtesy of wallygrom on Flickr.
Notes:
* For the absolute ideal efficiency, ![]() and as d=1
and as d=1 ![]()

