Can we measure encapsulation?

Detecting the undetected.

Something doesn't add up.

Most programmers value encapsulation, adhering to something like the ISO's definition by which encapsulation is the property that the information contained in an object is accessible only through interactions at the interfaces supported by the object.

Java programmers dig deep into the conceptual soil to bury functions within classes and classes within packages, leaving only interfaces fluttering above ground to announce the functionality below. Programmers do this because they know that good encapsulation reduces coupling which in turn reduces the cost of ripple-effects.

And reducing cost is simply what good programmers do.

How do we know, however, that a system is well-encapsulated? How do we know that a team which claims to write well-encapsulated software successfully achieves its goal? If encapsulation commands such time-hallowed respect, what are the precise objective criteria by which we measure it?

Janet works in a team producing on-line betting software. When asked, "Where is your encapsulation?" she responds, "Well, for example we don't want presentation-layer changes to affect anything in our database schema. So we've used plain-old MVC to separate our view from our model and controller, with our controller harvesting from the model the day's races, games and sporting events before calculating betting odds and feeding them to the view. We can change our betting-calculation algorithms, for example, by swapping implementation classes behind interfaces and again no changes ripple to other major subsystems. See? That's encapsulation. What's your problem? And why are you saying, 'Functions,' instead of, 'Methods?' You lookin' for trouble? Because I've got a whole bunch a trouble just waitin' to ENCAPSULATE ALL OVER YOUR ASS!"

(Prickly things, programmers.)

Janet is right. She has, aggression issues aside, described perfectly valid encapsulation. Her description, however, is both subjective and domain-specific.

It is subjective because she has provided no independent means of verifying her claims. We do not doubt her claims, pulsing as they do with vibrant MVC goodness, but another member of her team might give different reasons to explain why the system is well-encapsulated, or even - perish the thought - why it is not well-encapsulated.

In our search for the criteria by which encapsulation is measured we wish to avoid such subjectivity for obvious reasons.

Janet's description is domain-specific because she has used the semantics of on-line betting software to describe why she thinks her system well-encapsulated. This creates problems because we cannot transfer such semantics to, say, commercial aircraft simulation software or secure card-reading software, neither of which calculates Superbowl betting odds (very well).

Yet if we seek the criteria by which encapsulation is measured we wish these criteria applicable across a vast range of software; we refuse to cobble together bespoke criteria for each new domain. Here, again, we face the syntactic-vs-semantic problem: semantics shackle us to the particular whereas syntax scythes unblunted through all domains. We therefore seek a measure defined in terms of syntax only. In our case, the syntax is that of Java.

So, let us refine our question and ask: how do we measure encapsulation objectively and syntactically?

System's analysis.

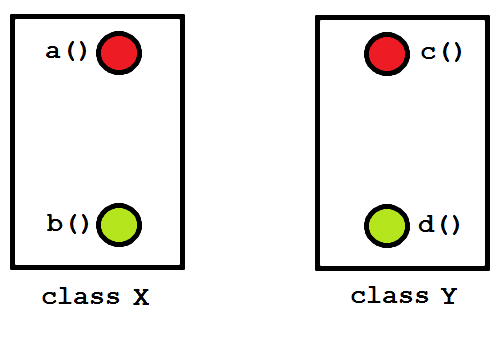
Figure 1: A basic system.

Figure 1 shows a system of two classes and four functions, functions being coloured red if they are public and green if private (we shall ignore the default and protected accessors for now). The system is, furthermore, devoid of problem-domain semantic information, the names of its elements being abstract. Let's make the system more realistic (ha!) by adding some dependencies, see figure 2.

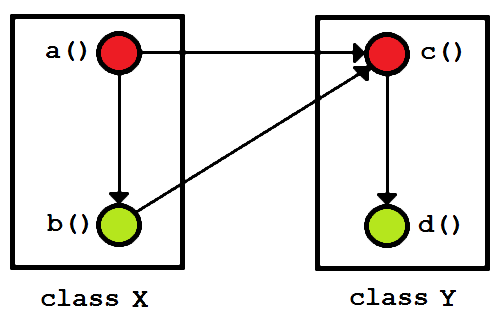
Figure 2: A hugely realistic improvement.

In figure 2, we see that, for instance, both a() and b() depend on class Y's public function c(), these dependencies being just a part of the system's function-level structure, that is, the set of its functions and the set of their inter-relationships. On class-level, we see that X depends on Y.

From this structure we can also read the system's coupling, the measure of the strength of association established by a connection from one module to another, which is that X is strongly coupled to Y in that X stands exposed to fifty per cent of Y's functions (albeit that fifty per cent is just one function).

So we can answer the question: what is the structure of this system? And, only slightly more vaguely, we can answer the question: what is the coupling of this system? But can we answer: what is the encapsulation of this system?

To help us see the difference between structure, coupling and encapsulation, let us try to alter the system such that its structure and coupling remain the same yet its encapsulation - whatever that is - changes.

Green to red.

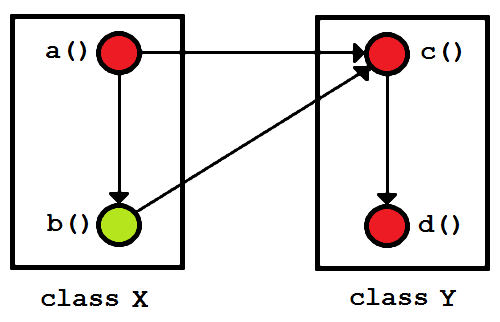
Figure 3: One function gone public.

In figure 3 we have changed the d() function from private (green) to public (red). Everything else is the same as figure 2.

The structure remains the same: figure 3 has the same number of functions and the same number of function dependencies as figure 2. The coupling remains the same: X is strongly coupled to Y.

But has the system's encapsulation changed?

If you asked a group of programmers whether the encapsulation of figure 2 differs from that of figure 3 many of them would probably say it does and furthermore that figure 3 is less well-encapsulated than figure 2.

That extra public method seems somehow problematic, wasteful. Why should it be public when there are no dependencies on it from without its class? The programmer clearly intended the function to be externally depended-upon yet then forged no such external dependency; intention and implementation diverged to the tolling of a mournful dissonance bell.

We perhaps struggle to express the specifics of how encapsulation has mutated between the figures but we can easily quantify one objective change: the number of possible dependencies has risen, that is, more dependencies could be established between functions in figure 3 than in figure 2.

In figure 2, it was not possible to form a dependency from a() to d() as d() was private; figure 3 welcomes such a dependency. We can even count the difference in the numbers of potential dependencies.

This countable property is called the, "Potential coupling." It measures the total number of dependencies that can be formed in a system regardless of whether those dependencies are actually formed. The potential coupling of any particular function is just the number of functions it can, "See," and given that it can see only co-located functions and those functions in other classes that are not information-hidden this property seems in tune with the ISO encapsulation definition above.

We also note that the relationship between potential coupling and encapsulation is an inverse one: more potential coupling implies less encapsulation (all else being equal).

Have we then found a quantitative, objective, syntactic measure of encapsulation?

Well, we can tell little from this single example; let us examine another scenario.

More, more, more.

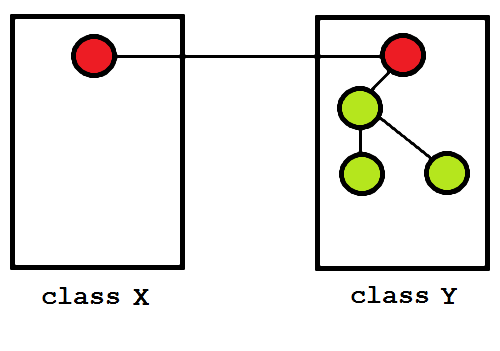
Figure 4: A yet more realistic system.

Figure 4 shows a new configuration of classes X and Y, now with X containing a single public function and Y containing one public and three private functions. Let us introduce yet another private function to this system, firstly in class X, see figure 5.

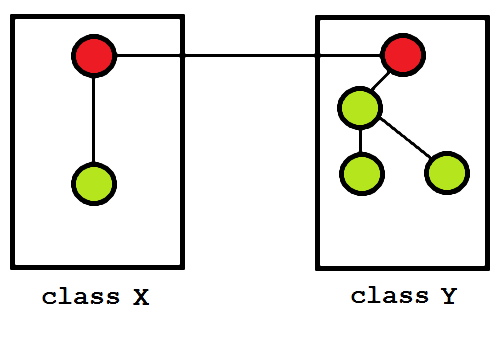
Figure 5: A new private function in X.

Now, in figure 6, we shall introduce the new function not in X but in Y. Thus figure 6 is an alternative to figure 5.

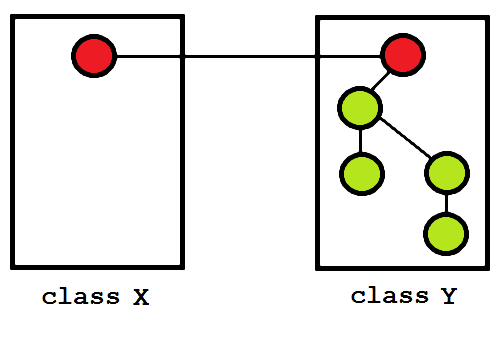
Figure 6: A new private function in Y.

So which is more well-encapsulated: figure 5 or figure 6?

Most programmers - once they stop objecting at the lack of semantic information which would surely be decisive - would probably say that, all else being equal, figure 5 is more well-encapsulated than figure 6. Figure 5 seems more balanced. In figure 6, class X looks disproportionately simplified and Y disproportionately complicated; X encapsulates too little, Y too much.

It turns out that figure 6 also has a higher potential coupling than figure 5. The counting is tedious but there are twenty potential dependencies in figure 5 and twenty-six in figure 6. The reason for this increase is that all the functions in Y, despite most being private, are nonetheless visible to one another and hence they can all form potential dependencies on one another.

A little set theory tells us that the number of potential dependencies that can form within any group of elements, where all elements are visible to one another, rises with the square of the number of elements whereas potential dependencies between groups obeys a linear relationship. Potential coupling thus flares dazzlingly when too many elements collect in a container, too many functions crushed into a class or classes into a package.

This, however, surely chimes with our general understanding of software design. Saddening police statistics confirm that oversized classes have a greater than average tendency to suffer attacks from vicious refactoring gangs, violence that leaves in its wake masses of smaller classes; similar misfortune regularly befalls bloated packages. Such antics merely reflect the studiousness with which some programmers observe the potential coupling principle, a principle which urges the eradication of unnecessary potential coupling where ever it is found.

So, again, a rise in potential coupling triggers concerns of encapsulation degradation. Have we found our measure?

Well, not quite. After all, as a system balloons its potential coupling must increase yet its encapsulation does not necessarily degrade. A large, well-encapsulated system can grow from a poorly-encapsulated seed.

How does potential coupling account for this?

Efficiency.

You might think that an article on encapsulation could not get any more boring, but wait!

As potential coupling is just glorified counting, we find, for example, that evenly distributing our functions over classes tends to minimize their potential coupling (as we saw above) ultimately giving us a minimum non-zero potential coupling, s_min. On the other hand, putting all functions in one class, or making all functions public, gives us a maximum potential coupling, s_max. A system's actual potential coupling, s_act, will usually lie somewhere between the two.

To any thermodynamics novitiate worth a Boltzmann brain these three values mean only one thing: efficiency. They allow us to measure how efficiently a Java program uses its potential coupling via the simple calculation:

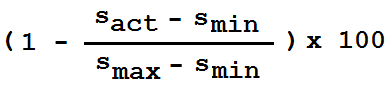
A system has an efficiency of 100% when its potential coupling is minimized and 0% when maximized. (In its overview, Spoiklin Soice shows this, "Absolute ideal efficiency," when the, "Potential coupling," analysis is active; the tool, by the way, has an efficiency of 69%.)

So, finally, are we there yet? Is this efficiency a measure of encapsulation?

Well ...

Summary.

Ultimately, our quest here was to failure doomed. Dominated by domain semantics, a concept as broad as encapsulation will always resist reduction to a single number. No doubt even a thousand years hence our software's encapsulation will still be judged by the fall of a reviewer's subjective gavel.

Yet with the above efficiency calculation we have a suggestion for a measure of encapsulation. A distant hint. An objective and syntactic whiff. Despite the measurement's tenuousness, some programmers have elevated it to a principle, whereby they strive to raise their system's efficiency ever higher through the ruthless eradication of unnecessary potential coupling. Such a principle does not obviate the reviewer's gaze but in the eternal battle against spiraling system costs, it helps.

And as they say:

Hokey reviews and ancient semantics are no match for a good principle at your side, kid.

Photo credit attribution.

CC image Holmes!!... courtesy of dynamosquito on Flickr.