• Blog
• Downloads
• Encapsulation
• Twitter
• RSS

Structure and theorems.

Travels though logic.

Look at this.

    void greet() {
	String hello = getHello();
	String subject = getSubject(1);
	showGreeting(hello, subject);
    }

    private String getHello() {
	return "Hello";
    }

    private String getSubject(int i) {
	if (i == 0) {
	    return "Fred";
	}
	if (i == 1) {
	    return "world";
	}
	return "everybody";
    }

    private void showGreeting(String hail, String subject) {
	System.out.println(hail + ", " + subject + ".");
    }

Tedious, ridiculously over-engineered Java code, but is it a theorem?

Trial by terminology.

First: what is a theorem?

Good, ol' wiki tells us that, "Logic ... considers theorems as statements (called formulas or well formed formulas) of a formal language. A set of deduction rules, also called transformation rules or rules of inference, must be provided. These deduction rules tell exactly when a formula can be derived from a set of premises." And further, "The initially accepted formulas in the derivation are called its axioms, and are the basis on which the theorem is derived."

That, "... derived from a set of premises," implies that theorems may be proved where, Wiki again, "A proof is a deductive argument for a mathematical statement," and further, "Deductive reasoning links premises with conclusions. If all premises are true, the terms are clear, and the rules of deductive logic are followed, then the conclusion reached is necessarily true."

What, then, is this curious beast, deductive reasoning?

Deductive reasoning.

When first learning deduction students usually face the syllogism in which a statement follows from two others:

1. All men are mortal.
2. Aristotle is a man.
3. Therefore, Aristotle is mortal.

This syllogism - the, "Mortal Aristotle," syllogism - boasts two premises, the first being that all men are mortal, the second that Aristotle is a man. It then offers a conclusion reached from these premises, namely that Aristotle is mortal. Given that most would consider, "All men are mortal," and, "Aristotle is a man," to be initially accepted statements (or, in the language of the Wiki definition, formulas), and given that Mortal Aristotle employs deduction to manufacture its conclusion, the syllogism would appear to fulfill all the criteria of theorem-hood. True, it may be a mere speck of a theorem, a homeopathic tincture of a theorem, but a theorem nonetheless it is.

Here, the investigation into whether source code can be a theorem might benefit from a temporary inversion: can this theorem Mortal Aristotle be written as source code? And of course it can.

    class Aristotle extends Man {
       .
       .
       .
    }

    boolean isMortal(Object object) {
	return object instanceof Man;
    }
    System.out.println(isMortal(new Aristotle()));

This code certainly looks the part. It has a Man, and an Aristotle and even something like a mortality deduction. That ugly instanceof should not distract the student from the method's epitomizing of deduction in its inferring the properties of things from the properties of other things. The form the code takes - the niceties of property inference - hardly matters; any number of alternatives would do as well. For example:

    boolean isMortal(Creature creature) {
	return creature.hasProperty(Property.Man);
    }

Or the method in the suggested Man class:

    @Override
    boolean isMortal() {
	return hasProperty(Property.MORTAL);
    }

Or even:

    @Override
    boolean isMortal() {
	return true;
    }

The core deduction remains.

But aside from demonstrating a certain arbitrariness of implementation, these examples fail to crystallize the core deduction. What device could humanity possibly have fashioned to carve sharp conclusion from such white marble premise?

In answer: humanity has in the depths of antiquity wrought a device of rare worth. This device presents us with that foundation of rational thought, that unshakably profound, that sonorously named, "Modus ponens."

Modus ponens.

Modus ponens, one of the few formal rules of deduction, allows the inference of a statement from other statements. Strong enough to heave the weight of an entire system of logic onto its broad shoulders, it finds expression in the form:

1. Statement P implies statement Q.
2. Statement P is true.
3. Therefore, statement Q is true.

These few lines expose deductive logic's essence: the first premise - the conditional - combines with the second premise to logically infer the conclusion. The conditional premise, furthermore, decomposes into the antecedent, P, and the consequent, Q. The second premise merely asserts P, the conditional's antecedent, while the conclusion infers the truth of Q, the conditional's consequent.

Both premises may either be true or false with modus ponens guaranteeing to preserve truth. If both the premises are true then the conclusion must be true. Thus Roars Modus Ponens.

In the wonderfully concise symbology of logic, where → indicates logical implication and ∴ indicates "therefore", modus ponens takes the following pleasing shorthand.

P → Q, P ∴ Q

This reads as, "Given that P implies Q is true and given that P is true, therefore Q must be true."

(Logic usually omits the, "Is true," settling for, "Given P implies Q and given P, therefore Q." Programmers celebrate their own histories here, usually interpreting the conditional as: if P then Q.)

Mortal Aristotle thus reveals itself as merely modus ponens in a pretty wig, and given that, as we saw above, Mortal Aristotle is one of the simplest forms of theorem, therefore each modus ponens, too, wears a, "Theorem," name tag. So can we extract from Mortal Aristotle the three definitive elements of modus ponens? The answer to this question ferries us to a central claim: a software method expresses the conditional premise of a modus ponens.

    class Aristotle extends Man {
       .
       .
       .
    }

    boolean isMortal(Object object) {
	return object instanceof Man;
    }
    System.out.println(isMortal(new Aristotle()));

In this case the conditional premise reads: an object's being an instance of the Man class implies its mortality. Or, in more programmer-friendly if-then guise: if an object is an instance of the Man class then that object is mortal. The actual machinery of realizing this conditional involves the semantics of the method's name and every last scrap of its arguments, body and return value.

The class structure itself captures the second premise, though as seen above such specifics do not constrain generality. The Aristotle class's deriving from the Man class thus asserts: an Aristotle object is an instance of the Man class.

The final part, the conclusion, warps curiously when projected from the language of logic to computer code because Java models this particular inference from premises, and hence the reaching of conclusions, as a method invocation. Thus, the conclusion is the run-time result of: evaluate the isMortal() method with an Aristotle object.

So, with the modus ponens structure mapped to the Mortal Aristotle source code, attention can now turn from Mortal Aristotle towards an attempt at similar a mapping in the source code with which this post opened.

The getHello() theorem.

The getHello() method takes stage first, taking no arguments and always returning the same string value, "Hello".

    private String getHello() {
	return "Hello";
    }

Could this be a theorem? Does it express the conditional premise of a modus ponens? And if so, what are its premises and conclusion?

In this case the conditional premise appears oddly unconditional, namely that, irrespective of all else, the method returns, "Hello". This method differs crucially, however, from the Mortal Aristotle source code in that isMortal() exemplifies a predicate, that is, it evaluates based on its arguments to true or false and nothing else. Predicates share this true/false dichotomy with statements, both being logical entities over which modus ponens happily operates, neither of which ever evaluates to anything as unruly as a String.

Fortunately, investigations into the logic of source code take place in parallel with the source code itself by the making of statements about what the source code does. In this case, the statement can be made that the method evaluates to "Hello" under all circumstances, a statement that evaluates to true or false. Logicians capture the invariability of this implication via the phrasing: if true then evaluates to "Hello". The method expresses this invariability by its taking no arguments: it will return the, "Hello", string on invocation, each and every time.

The method's second premise expresses itself by omission in that it requires neither data nor logical structure to establish itself. Recall that the second premise merely apes the if statement of the conditional, which the above found to be the constant, true. As true remains always and invariably true, the method's taking no arguments effectively maps to a second premise of, simply: true.

In similarly trivial vein, the system establishes the veracity of asserting both premises to yield a conclusion via the method's invocation without arguments. This yields the conclusion: evaluates to "Hello" and thus the method as a whole takes the following logical form.

getHello() = true → evaluates to "Hello", true ∴ evaluates to "Hello"

We interpret this as: given that true implies that getHello() evaluates to "Hello" and given true, then getHello() evaluates to "Hello". The below is the syllogistic format.

getHello()=

1. true → evaluates to "Hello"
2. true
3. ∴ evaluates to "Hello"

We can now reason about this method, analyzing whether it preserves truth by asking the question: given true does invoking this method evaluate to "Hello"? Or, slightly reduced: true, getHello() == evaluates to "Hello"? To which we can answer: hell, yes.

If there had been anyone still reading at this point, that reader would have considered the above an eye-wateringly absurd exercise in the obvious. Yet this very absurdity serves a purpose as it seems absurd only in its being a pointless re-statement, lacking value or insight, of the original method. This syllogism, however, represents pure logic; and if it derives unmolested from source code then that source code must also represent pure logic, thus going quite some way towards answering the question of the introduction.

The getSubject() theorem.

    private String getSubject(int i) {
	if (i == 0) {
	    return "Fred";
	}
	if (i == 1) {
	    return "world";
	}
	return "everybody";
    }

The method getSubject() offers a slightly more realistic example of programming than does Mortal Aristotle. Does it express the conditional premise of a modus ponens? Does it have an antecedent and a consequent? Indeed it does.

The antecedent is the predicate that the value of the argument, i, is an integer which is 0 or 1 or it is neither 0 nor 1. That is, i enjoys membership of the set of values {0, 1, neither(0, 1)}, which shorthand compresses to: i ∈ {0, 1, neither(0 or 1)}. A predicate of i, this evaluates to true or false precisely as the modus ponens antecedent must. (To avoid excessive detail we have not written that third element as i being a member of a set excluding other values; the student should take that, "neither," rather on face value. Actually, computer systems cannot enumerate over the set of integers, which span infinite range, so plenty of salt-pinching and glossing-over going on here with apologies to logicians everywhere.)

The consequent expresses that this method evaluates to some value, x, which is either "Fred" or "world" or "everybody"; that is, it evaluates to x | x ∈ {"Fred", "world", "everybody"}. (That vertical bar reads as, "Such that," so an informal translation of this consequent would be, "This method evaluates to some value x such that this x is either "Fred" or "world" or "everybody".") These six terms do not, of course, map haphazardly onto one another; only a particular value of i maps to a particular evaluation. Again, to keep this post manageable, the set-to-set mapping will have to suffice, leaving element-to-element mappings as an exercise for the student.

The getSubject() method thus takes its place as the conditional premise in the syllogism:

getSubject(i)=

1. i ∈ {0, 1, neither(0 or 1)} → evaluates to x | x ∈ {"Fred", "world", "everybody"}
2. i ∈ {0, 1, neither(0 or 1)}
3. ∴ evaluates to x | x ∈ {"Fred", "world", "everybody"}

Annoying pedantry time again. We can now reason about this method, establishing the truth of the question: given i ∈ {0, 1, neither(0 or 1)} does invoking this method evaluate to x | x ∈ {"Fred", "world", "everybody"}? And again slightly reduced: i ∈ {0, 1, neither(0 or 1)}, getSubject(i) == evaluates to x | x ∈ {"Fred", "world", "everybody"}? To which we can safely argue: yes.

The showGreeting() theorem.

    private void showGreeting(String hail, String subject) {
	System.out.println(hail + ", " + subject + ".");
    }

showGreeting() differs from getHello() in that it takes arguments but returns no value. This once more presents little difficulty, logicians claiming that, "Returns no value," translates to the trivial logical case of the method's always evaluating to: true.

Thus showGreeting() can still be viewed as the conditional premise of a modus ponens theorem with the conditional's antecedent being that the two arguments, arg1 and arg2, are Strings. This method, therefore, has a compound statement as an antecedent: that arg1 is a String and arg2 is a String. Borrowing from logic symbolism again and using ∧ as the symbol for logical AND then we can write this compound statement as: arg1 ∈ String ∧ arg2 ∈ String.

But what of the System.out.println() statement? Is it a theorem? How does this fit into the puzzle?

Here, the investigation distinguishes between the source code under examination and the system functions supporting that source code. The source code can be considered, "Internal," and the focus of attention. The supporting system functions can be considered, "External," and, despite their obvious importance, uninteresting. Logicians gladly claim such external functionality to reside, "Outside the domain of discourse," where this domain's boundaries - as the domain boundaries of all logical endeavors - are agreed upon but ultimately arbitrary, the goal being self-consistency rather than completeness. Essentially, we shall ignore all calls to functionality outside the source code.

The conclusion of this theorem, then, guarantees to evaluate at all times to: true and so yields the following syllogistic format.

showGreeting(arg1, arg2)=

1. arg1 ∈ String ∧ arg2 ∈ String → true
2. arg1 ∈ String ∧ arg2 ∈ String
3. ∴ true

The greet() theorem.

    void greet() {
	String hello = getHello();
	String subject = getSubject(1);
	showGreeting(hello, subject);
    }

greet() tosses together the theorems so far examined and unearths the somewhat loose distinction between axiom, lemma and theorem. We shall consider a method an axiom if it depends on no other internal theorem for its logical integrity. Thus all theorems studied so far are axioms in that they may depend on external theorems (supporting system functions outside the domain of discourse) but internally they stand self-contained and depend on none. In its independence the axiom expresses a simplicity sufficient, hopefully, to render it, "Initially accepted," to all. A method shall be a lemma if it depends on other methods and other methods depend on it whereas a method shall be a theorem only if no other methods depend on it.

greet() then presents our first true theorem, as opposed to an axiom, in its obvious dependence on other internal axioms within the source code in question. But how do we logically analyze greet()? Is it too a modus ponens?

Taking no arguments and returning no values, greet() appears to have both conditional antecedent and consequent as merely true, tempting the rather dull interpretation:

greet() = true → true

Recall, however, that Java models inference assertion through method invocation. Thus calling methods within greet() implies the expansion of the antecedent to do some further heavy lifting and to incorporate the assertion of all its invoked methods.

greet() essentially invokes showGreeting() with specific arguments, the first being returned from getHello(), the second from getSubject(). From the logical point of view getHello(), getSubject() and showGreeting() are statements or predicates that evaluate to true or false as we have already seen in indigestible detail. greet() must make those assertions and combine them to generate its own true or false, a combination achieved by logically ANDing the three axioms to derive their amalgamated truth. This leads to the deeply unfortunate splurge of logic as follows.

greet() = (true, getHello() == evaluates to "Hello") ∧ (1 ∈ {0, 1, neither(0 or 1)}, getSubject(1) == evaluates to x | x ∈ {"Fred", "world", "everybody"} ) ∧ (getHello() ∈ String, getSubject(1) ∈ String, showGreeting(getHello(), getSubject()) == true) → true

The monstrous syllogistic form is even worse.

greet()=

1. greet() = (true, getHello() == evaluates to "Hello") ∧ (1 ∈ {0, 1, neither(0 or 1)}, getSubject(1) == evaluates to x | x ∈ {"Fred", "world", "everybody"} ) ∧ (getHello() ∈ String, getSubject(1) ∈ String, showGreeting(getHello(), getSubject()) == true) → true
2. greet() = (true, getHello() == evaluates to "Hello") ∧ (1 ∈ {0, 1, neither(0 or 1)}, getSubject(1) == evaluates to x | x ∈ {"Fred", "world", "everybody"} ) ∧ (getHello() ∈ String, getSubject(1) ∈ String, showGreeting(getHello(), getSubject()) == true)
3. ∴ true

Naturally, no sane programmer views programs like this. Furthermore - Hoare and Dijkstra notwithstanding - few recommend doing so. This, again, hardly matters: programs can be viewed so. They can be viewed so because an equivalence exists between the traditional theorematic and the programmatic representations of the underlying logic at play. This equivalence forms the cushion on which sits comfortably the claim that, in their both capturing the same logic, programs are theorems. Not only this but programs embody some of the most powerful and fantastically intricate theorems ever conceived by the human species, with programmers history's matchless logicians.

Theorems in the digital wild.

To drag us back to developer reality, let us bathe in the source code of a randomly-selected open-source product. In July, 2013, Apache released the latest version of Lucene, their popular text search engine. Figure 1 presents a spoiklin diagram of the core Lucene jar, in which a circle represents a method.

Figure 1: Lucene

The above pollockian chaos results from splattering all 9214 methods onto a single canvas and trickling a thin grey line to represent each of the 127,000 transitive dependencies. These dependencies draining down the page, the diagram shows all the methods that are theorems at the top, smeared into a rather uninformative horizontal band. The lower black methods indicate axioms, dependent on no others, the white and red methods indicate lemmas, both depended-on and dependent.

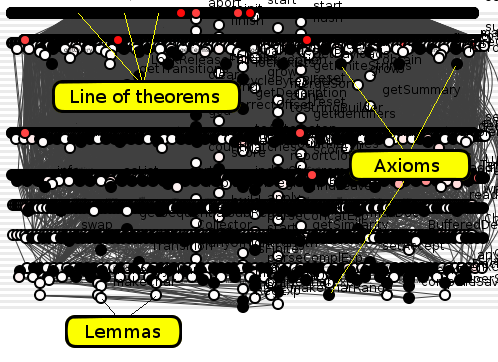
Figure 2: Lucene with components highlighted

So how many theorems constitute this real-world, business-critical software? 4289. Lucene makes 4289 statements about reality and in making those statements the world gains a new text search engine.

Let us take a closer look at any Lucene method, say getTerms() below.

    /**  This method may return null if the field does not exist.*/
    public static Terms getTerms(IndexReader r, String field) 
	throws IOException {
	final Fields fields = getFields(r);
	if (fields == null) {
	    return null;
	} else {
	    return fields.terms(field);
	}
    }

With our theorem spectacles on, we see that this method clearly derives from other theorems and axioms within the Lucene source code. Figure 3 captures this derivation with filled circles representing internal axioms.

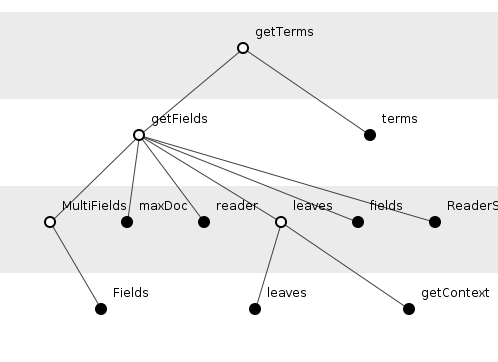
Figure 3: getTerms() derivation

getTerms() derives from eight axioms, three lemmas. Is getTerms() itself a theorem or a lemma? It turns out to be a lemma, the theorems deriving from it shown in figure 4, this time with the theorems highlighted as filled circles.

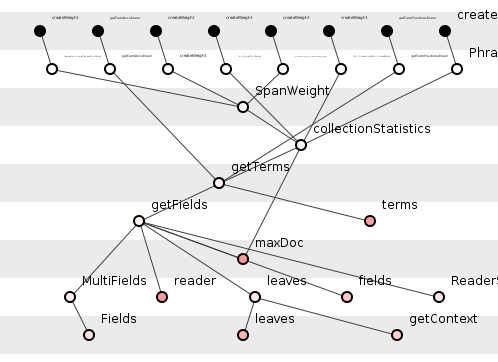
Figure 4: getTerms() in full context

Eight theorems derive from getTerms(), establishing their truths from its.

So, is a program a set of theorems?

We say again: hell, yes.

Summary.

Doctor Who is a Time Lord.

He travels through space and time in a blue box called a TARDIS.

The BBC sent a documentary film-crew with the Doctor during his visit, back in 1981, to the planet Logopolis, where they reported on a civilization that created matter from pure mathematics on the basis that, as one announced to camera, "Structure is the essence of matter and the essence of structure is mathematics."

Similarly, the structure of modern programs reveals them to be gigantic gargoyle-encrusted cathedrals of logic, with thousands upon thousands of theorems making bold statements derived from thousands upon thousands of lemmas and axioms, generating - magically and from sheer expression of logic alone - the digital products without which modernity would be unthinkable.

Is not this astonishing?

Photo credit attribution.

CC image Tardis_Trans courtesy of The Daring Librarian on Flickr.

CC image Vwooorp courtesy of subberculture on Flickr.

CC image DSC_0119_2 courtesy of swamp dragon on Flickr.