
The ripple hypothesis.
Perhaps this blog's most quoted passage, a single paragraph from a 1974 paper forms the basis for essentially all software structure:
"The fewer and simpler the connections between modules, the easier it is to understand each module without reference to other modules. Minimizing connections between modules also minimizes the paths along which changes and errors can propagate into other parts of the system, thus eliminating disastrous, 'Ripple effects,' where changes in one part cause errors in another, necessitating additional changes elsewhere, giving rise to new errors, etc."
The authors understand the changes to propagate from modules depended-on to depending modules, as they later write, "For example, only two modules ... might make use of data element X in an 'included' common environment ... yet changing the length of X impacts every module making any use of the common environment."
But is this true?
Do ripple effects exist1? Are they supported by empirical evidence, or do we just take them on faith? And if they exist, do they really propagate from depended-on to depending modules?
Let's get down'n'geeky.
Let m be any method of program S.
Let Cm be the set of methods that m directly depends on, the children of m.
Let Am be the set of methods that directly depend on m, the antecedents of m.
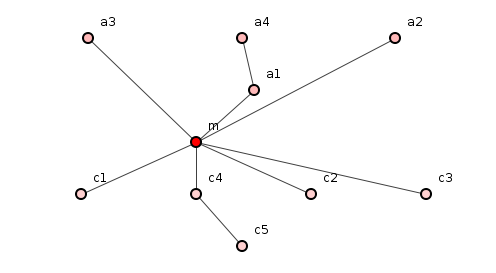
Figure 1: With dependencies drawn downwards, Am = {a1, a2, a3}, the antecedents of m, while Cm = {c1, c2, c3, c4}, the children.
Let's define function δ() as identifying change, where a "change" is a difference in compiled bytecode between two consecutive revisions. So δ(m) is a change in method m between two revisions. We can then define the conditional probability of the change in m given a change in any of its children over all consecutive revisions, namely:
P(δ(m) | δ(Cm))
Similarly we can define the probability of a change in m given a change in any of its antecedents:
P(δ(m) | δ(Am))
Then the ratio of the two defines the ripple bias of m, Rm:
| P(δ(m) | δ(Cm)) | |
| Rm = |
|
| P(δ(m) | δ(Am)) |
We can stretch this to the ripple bias of the entire system by averaging probabilities over all methods in S:
| P(δ(m) | δ(Cm)) | ||
| RS = |
|
∀ m ∈ S |
| P(δ(m) | δ(Am)) |
If ripple effects bubble up from children then this ratio will be greater than 1; if they tumble down from antecedents, it will be less than 1. If nothing but a programmer's pizza-fueled imagination gave fevered birth to ripple effects one lonely Winter's night, this ratio will be almost exactly 1.
So let's make the bold claim that the average ripple bias for a large collection of n programs is greater than 1, that is, for k=1..n:
RSk > 1
This is the ripple hypothesis. It claims that ripple effects exist and they leap from depended-on to depending methods. The question however remains: is it true?
Fortunately, this mathematical treatment allows us to measure2 approximate probabilities using real Java code, if sufficiently large numbers of measurements are made on sufficiently large numbers of changes. Thus, 64 million lines of Java were analyzed as 20 programs ground through 22 thousand revisions (details here). The measured ripple bias suggests that the hypothesis is indeed true:
RSk = 1.5
That is, ripple effects exist and are 50% more likely to ripple up than down4, 5, 6.
This fundamental asymmetry at the heart of software structure exerts profound influence. For the ripple hypothesis makes two further measurable predictions.
Firstly, given a changed method, the number of changes it undergoes should correlate more with its number of children than with its number of antecedents. (A correlation is a number between -1 and +1, where +1 suggests a strong connection between two sets of data and 0 suggests no connection whatsoever.)
Measuring the same codebase above confirms this: the average changed method has a correlation of 0.28 with its number of children, but just -0.01 (essentially negligible) with the number of its antecedents.
Secondly, if children primarily trigger ripple effects then it follows that a method with no children - a method that depends on no other, an "independent" method - should suffer fewer changes than a method that does depend on others - a "dependent" method.
It was found, measuring the codebase again, that this is the case: dependent methods, per line of code, are a whopping 92% more likely to change than independent methods.
Most programmers will find all this tediously obvious, so why bother with this analysis?
Two reasons.
Firstly, it offers a perspective shift.
Figure 2, presented many times before, shows a poor structure on the left and the improved version on the right with reduced depth, refactored according to the SIP-TD principles.
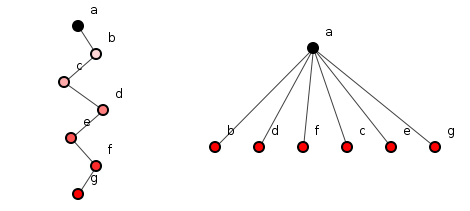
Figure 2: A deep transitive dependency on the left, and shallow "sunburst" dependencies on the right.
The ripple hypothesis allows us a slightly different interpretation. Instead of seeing the figure on the right as a depth-reduction, we can appreciate it as a maximization of the number of independent methods: the figure on the left has 1 independent method, the figure on the right boasts 6. And as independent methods suffer fewer ripple effects, the right-hand configuration should be cheaper to change.
Secondly, it offers objective evidence to defend programmers in their choice of code structure.
When a code reviewer asks why you structured your code in a certain way, it's fine to say, "Because of the Single Responsibility Principle," but be prepared to argue what responsibility you mean, how many others there are, and whether you've prioritized the list as would the reviewer. If, however, you're asked why you have one method calling many, you can always say, "Because an analysis of 64 million lines of code showed that independent methods cost less."
(Mic drop.)
This investigation, furthermore, focused on methods, but there is no reason to assume that ripple effects fail to haunt class- and package-levels as well. So if the ripple hypothesis is sound then, to paraphrase Spock, we would be wise to accept its conclusion. Namely, pepper your code with sunbursts at all levels. The finance department will thank you*.
(The observant among you will have spotted a slightly disturbing implication of all this, an implication to be explored in the next post.)
*The finance department won't thank you. They don't thank anyone. Bean-counters!